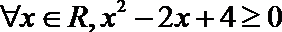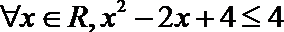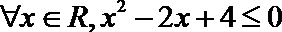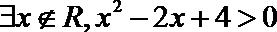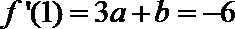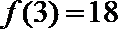- 真题试卷
- 模拟试卷
- 预测试卷
4.下列函数中,既是奇函数又是增函数的是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.命题“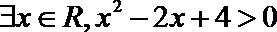
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.要得到函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知向量


正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
12.首项为1,公比为2的等比数列的前4项和
正确答案
15
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14 ~15题,考生只能从中选做一题)
14.(坐标系与参数方程选做题)已知圆
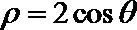

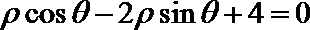
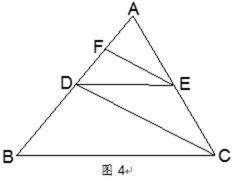
15.(几何证明选讲选做题)如图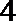
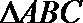
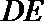
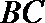
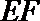
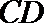

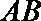
正确答案
14.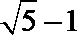
15.4
解析
解析已在路上飞奔,马上就到!
知识点
13.已知{an}为等差数列,Sn为其前n项和,若
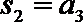

正确答案
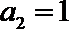
解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列




(1)求数列
(2)设




正确答案
(1) 解:设数列



解之得:


(2)证明: ∵


①-②得:
得
∵
∴

∴
而

又
综上所述,
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)当



(2)若


正确答案
(1)当
得
令
解得
所以函数
据此,函数
而
所以函数
(2)由
当
函数
当
函数

由
和
得
若

此时,
只需

所以
综合上述,实数
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数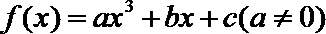
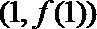
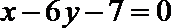
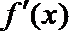
(1)求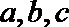
(2)求函数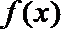
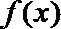
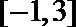
正确答案
(1)∵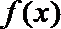
∴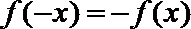
∴
∵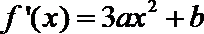
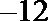
又直线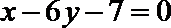

∴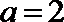
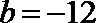
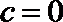
(2)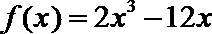
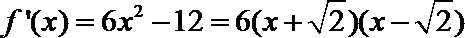
所以函数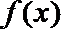
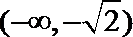
∵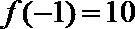
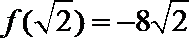
∴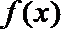
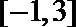
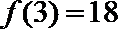
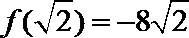
解析
解析已在路上飞奔,马上就到!
知识点
18.育才中学文科班某同学参加广东省学业水平测试,物理、化学、生物获得等级









(1)试列举该同学这次水平测试中物理、化学、生物成绩是否为


(2)求该同学参加这次水平测试获得两个
(3)试设计一个关于该同学参加这次水平测试物理、化学、生物成绩情况的事件,使该事件的概率大于
正确答案
(1)该同学这次水平测试中物理、化学、生物成绩是否为

分别为







(2)由(1)可知,有两个A的情况为


从而其概率为
(3)方案一、该同学参加这次水平测试中物理、化学、生物成绩不全为

理由如下:该同学参加这次水平测试中物理、化学、生物成绩不全为







概率是
方案二、该同学参加这次水平测试中物理、化学、生物成绩至少一个

理由如下:该同学参加这次水平测试中物理、化学、生物成绩不全为








解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量


(1)求函数
(2)当

(3)说明

正确答案
(2)由
解得
∵取k=0和1且


∴


法二:∵

∴由

解得

∴


(3)



再把所得各点的横坐标缩短到原来的
最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),
得到
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)设



正确答案
(1)由

故

(2)由


且α是第二象限的角, 解得



故




解析
解析已在路上飞奔,马上就到!