- 真题试卷
- 模拟试卷
- 预测试卷
2.已知向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.等差数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知一实心铁质的几何体的正视图、侧视图和俯视图都是半径为3的圆,将6个这样的几何体熔化成一实心正方体,则该正方体的表面积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如下图,


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知正



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数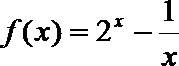
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.存在正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.等比数列



正确答案
27
解析
解析已在路上飞奔,马上就到!
知识点
15.平面向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.计算:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知集合M是满足下列条件的函数
(1)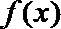
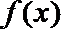
①
②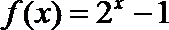
③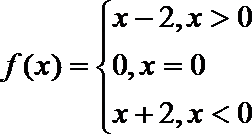
④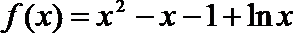
属于集合M的有( )(写出所有符合条件的函数序号)
正确答案
②、④
解析
解析已在路上飞奔,马上就到!
知识点
18.已知数列


(1)求证:数列
(2)求数列

正确答案
(1)∵
∴
又
∴
∴数列
(2)由(1)知数列
∴
∴数列
解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列



(1)求数列

(2)令


正确答案
(1)∵
∴当
又当

∴数列
又∵
∴当
∴
又当

∴数列

∴数列
(2)∵
∴
∴当
∴当且仅当

解析
解析已在路上飞奔,马上就到!
知识点
19.右图为一长方体截去一个角后所得多面体的直观图以及它的正视图和侧视图.
(1)按三视图的作图要求画出该多面体的俯视图;
(2)按给出的尺寸,求该多面体的体积。
正确答案
(1)按要求作出俯视图得分
(2)由图可知,所求多面体的体积为长方体体积减去一三棱锥的体积
∴
∴该多面体的体积为
解析
解析已在路上飞奔,马上就到!
知识点
17.已知


(1)
(2)
(3)
正确答案
(1)∵
∴
∴
∴当

(2)∵
∴
解得:
∴当

(3)∵
∴
解得:
∴当

解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)求函数
(2)若当


(3)若关于



正确答案
(1)由函数

∵
令


∴函数

(2)由题意知不等式

∴
∴令
当

∴
又
∴
∴
∴实数
(3)依题意:关于


即方程

∴化简得方程

令
∴
令
∴当


∴函数


∴要使方程


解得
∴实数

解析
解析已在路上飞奔,马上就到!
知识点
21.已知数列

(1)求数列
(2)是否存在等差数列



正确答案
(1)由已知条件可得:
设数列

∴数列

(2)假设存在等差数列


则
将以上两式相减得:
∴
又
∴
∴
∴存在等差数列


解析
解析已在路上飞奔,马上就到!