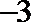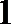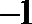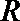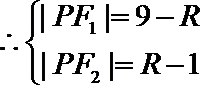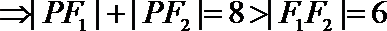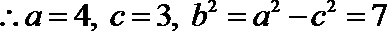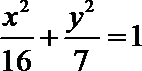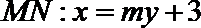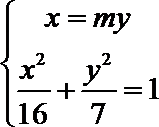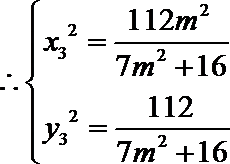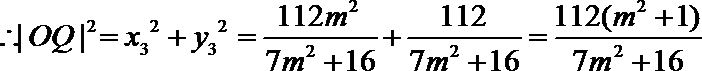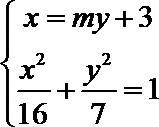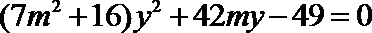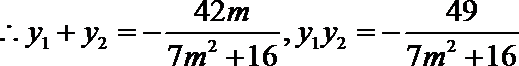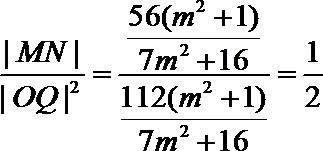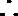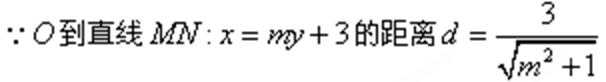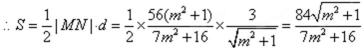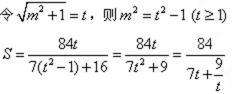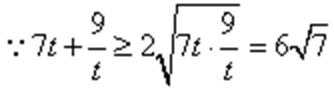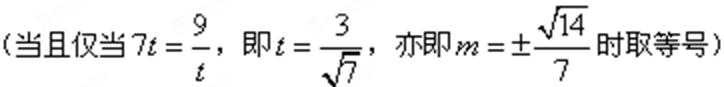- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数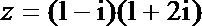
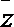
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.如图是一个算法的流程图.若输入


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.某防疫站对学生进行身体健康调查,欲采用分层抽样的办法抽取样本。某中学共有学生


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知三棱锥





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某四棱锥的三视图如图所示,记A为此棱锥所有棱的长度的集合,则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知偶函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.在平面直角坐标系中,







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知点




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如图,





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.抛物线
正确答案
(0,1)
解析
解析已在路上飞奔,马上就到!
知识点
12.已知







正确答案
70
解析
解析已在路上飞奔,马上就到!
知识点
15.对于下列命题:其中所有真命题的序号是___________
① 函数


② 已知



③“


④“

正确答案
①②④
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,在四棱锥






(1)求证:

(2)求四棱锥
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)从区间





(2)若连续掷两次骰子(骰子六个面上标注的点数分别为






正确答案
(1)




即

(2)由已知:
所以
即




当


当


当


满足

而基本事件总数为

解析
解析已在路上飞奔,马上就到!
知识点
19.已知数列

(1)令


(2)记



正确答案
(1)
即





(2)对于
当
即



当
可得




解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数



(1)若




(2)求

(3)试探究能否存在区间







正确答案
(1)
(2)
(3)
②若

在


在


由于






综上,当

使得


当




解析
解析已在路上飞奔,马上就到!
知识点
21.已知动圆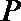
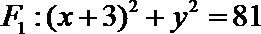
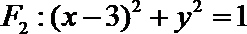
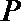
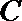
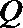
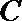

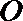
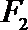
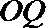
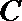
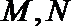
(1)求曲线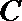
(2)试探究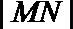
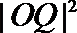
(3)记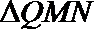


正确答案
(1)设圆心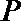
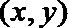
由于动圆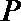
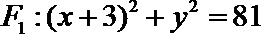
且与圆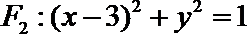
圆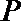
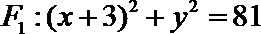
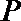
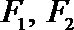
其中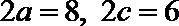
故圆心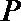
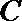
(2)设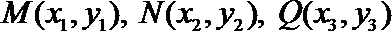
直线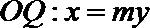
由
可得: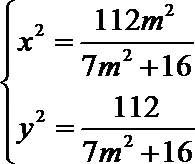
由
可得:
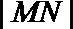
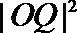
(3)
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数

(1)求函数
(2)若函数




正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!