- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集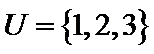
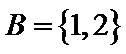
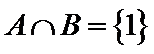
正确答案
解析
因为A中必含有元素1,不含元素2,可能含有元素3,所以共有2个满足题意的集合。
考查方向
解题思路
利用交集只有1这一个元素,然后集合A中必然含有元素1,不能含有元素2,然后分别举出所有的情况。
易错点
1、容易漏掉集合A里面的元素或者考虑问题的时候比较片面,出现集合A里面多出一个元素2。
知识点
2.复数的虚部是 ( )
正确答案
解析

考查方向
解题思路
分母进行实数化,分母乘以它的共轭复数,化简之后找到虚部。
易错点
1、不知道怎样进行化简,也就是对这个式子进行分母实数化。
2、对虚部这个概念容易搞错,有些同学可能会把i也会认为是虚部里面的导致错误。
知识点
3. 下面的程序框图(如图所示)能判断任意输入的数

正确答案
解析
m是这个数除以2所得的余数,往左边是这个方向输出的是奇数,所以奇数除以2的余数为1,故选D。
考查方向
解题思路
根据奇数和偶数除以2所得的余数为0还是1来判断。
易错点
1、不知道是在判断框里面填什么,不知道是m为0还是填x为0。
知识点
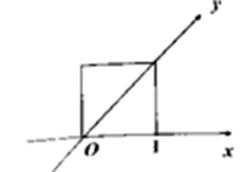
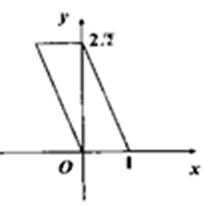
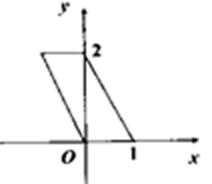
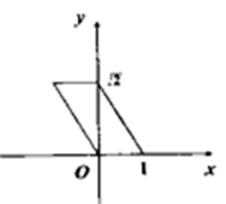
4. 用斜二测画法画一个水平放置的平面图形为如下图的一个正方形,则原来图形的形状是( )
正确答案
解析
在x轴上的线段不变,先找到在y轴上的那一点,回到原图的时候要变为2倍,原来与x轴平行的线段在画原图的时候仍然保持与x轴平行且长度不变,故A正确。
考查方向
解题思路
反过来由直观图变为原图的时候x不变,y变为2倍。
易错点
1、在y轴上或者与y轴平行的线段在直观图中不知道变为原来的一半。
知识点
7. 数列{an}的通项公式an=ncos,其前n项和为Sn,则S2016等于( )
正确答案
解析
其中所有的奇数项都为0,而偶数项是分别为第二项是-2,第四项是4,第六项是-6,第八项是8,这样可以将每2项相加放在一起,刚好有1008个偶数项,即可以组成504组,每组的值为2,所有答案就为1008,故A正确。
考查方向
解题思路
算出前4项并找到这个数列的规律,最后用求和公式解决。
易错点
1、不能找到数列的周期性,没有找到规律导致无法计算下去。
知识点
8.O是平面上一定点,A、B、C平面上不共线的三点,动点P满足
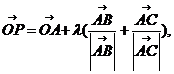
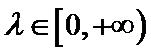
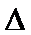
正确答案
解析
由已知可得
考查方向
解题思路
将已知的等式化简,根据向量共线基本定理找到AP是在三角形的角平分线上。
易错点
1、不能根据已知的等式将其化简。
知识点
10. 设椭圆






正确答案
解析
在直角三角形


考查方向
解题思路
根据焦距为2c,在直角三角形中将其他两边用c表示出来,再利用椭圆的定义得到一个等式,解出比值就可以得到所求的离心率。
易错点
1、根据已知条件不能转化为a,b,c有关的一个等式。
知识点
11. 如图,有一圆柱开口容器(下表面封闭),其轴截面
正确答案
解析
如图,展开后作辅助线,使得QC=CP,则AQ即为所求最小距离,利用勾股定理可得D选项是正确的。
考查方向
解题思路
将图像展开之后,通过等价转化,最后变成两点间的距离来求解。
易错点
1、不知道怎样将圆柱展开。
知识点
12.已知函数




正确答案
解析



考查方向
解题思路
根据函数的导函数恒大于等于零最后转化为求函数的最值问题。
易错点
1、不能通过函数的导函数来解决问题。
知识点
5. 经过抛物线x2=4 y的焦点和双曲线-=1的右焦点的直线方程为( )
正确答案
解析
抛物线的焦点坐标是(0,1),双曲线的焦点是(5,0),两点式方程写出所求直线的方程再化为直线方程的一般式可得D选项。
考查方向
解题思路
求出抛物线的焦点和双曲线的焦点坐标,然后用两点式方程求出即可。
易错点
1、容易求错抛物线的焦点坐标。
知识点
9. 函数y=-x·cosx的部分图象是( )
正确答案
解析
由于函数是一个奇函数,所以可以排除选项A,C,然后将
考查方向
解题思路
根据函数的奇偶性,然后可以根据特殊值来确定函数的图像。
易错点
1、不能通过函数的性质去解决问题。
知识点
已知等差数列{an}的公差不为零,a1=25,且a1,a11,a13成等比数列.
18.求{an}的通项公式;
19.求a1+a4+a7+…+a3n-2.
正确答案
an=-2n+27,(2)Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
解析
解: (1)设{an}的公差为d.由题意,a=a1a13,[即(a1+10d)2=a1(a1+12d), 于是d(2a1+25d)=0.又a1=25,所以d=0(舍去),或d=-2.故an=-2n+27
考查方向
解题思路
本题考查等差数列和等比数列,数列的求和,解题步骤如下:设出等差数列的公差,由已知等比数列构造出一个方程解出符合题意的公差,写出数列的通项公式。
易错点
求和的时候将里面的项数弄错,等比中项性质。
正确答案
Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
解析
令Sn=a1+a4+a7+…+a3n-2.由(1)知a3n-2=-6n+31, 故{a3n-2}是首项为25,公差为-6的等差数列.
从而Sn=(a1+a3n-2)=·(-6n+56)=-3n2+28n.
考查方向
解题思路
要求的数列也是一个等差数列,利用等差数列的前n项和公式解答即可。
易错点
求和的时候将里面的项数弄错,等比中项性质。
20.求点B到面
正确答案

解析
在














考查方向
解题思路
由等体积法计算出点到平面的距离。
易错点
不知道由线面垂直转化为证明线线垂直,等体积求距离。
正确答案
见解析
解析
考查方向
本题考查了线线垂直的证明,点到平面的距离求解.
解题思路
由线面垂直的判断定理先判断线面垂直,由线面垂直得到线线垂直,
易错点
不知道由线面垂直转化为证明线线垂直,等体积求距离。
设







21.当


22.求过点



正确答案

解析
设M的坐标为






考查方向
解题思路
由相关点法求轨迹方程,
易错点
不能想到相关点法求轨迹方程,设而不求的思想即弦长公式利用。
正确答案

解析










考查方向
解题思路
由弦长公式求弦长。
易错点
不能想到相关点法求轨迹方程,设而不求的思想即弦长公式利用。
已知函数f(x)= 

25.求函数f(x)的最小正周期及单调减区间;
26.把函数f(x)的图像向右平移
正确答案
T=



解析
f(x)=sin(2x-2φ)-+=sin(2x-2φ)-cos(2x-2φ)=sin(2x-2φ-

















解题思路
先用二倍角公式和降幂公式化简,然后用辅助角公式合二为一,再求最小正周期和单调减区间
易错点
降幂公式不会用,忘记写k属于整数,对称中心不知道写成点的坐标的形式。
正确答案
g(x)的对称中心为(
解析
函数f(x)=-cos2x的图像向右平移







考查方向
解题思路
利用平移变换左加右减得到另一个函数的解析式,再求出其对称中心。
易错点
降幂公式不会用,忘记写k属于整数,对称中心不知道写成点的坐标的形式。
已知函数
23.若

24.求证:


正确答案



解析
















考查方向
解题思路
利用数形结合去做。
易错点
导数的运算法则,不等式的证明。
正确答案
见解析.
解析











当







考查方向
解题思路
利用数形结合去做。
易错点
导数的运算法则,不等式的证明。
17.在△ABC中,B=

正确答案
△ABC是等边三角形.
解析
试题分析:本题属于解三角形的基本问题,(1)直接按照已知条件转换成关于角C有关的表达式,最后将式子化简后来求.
在△ABC中,根据
得
同理BC=2sinA,因此AB+BC=2sinC+2sinA
因此AB+BC的最大值为

考查方向
解题思路
本题考查正弦定理和三角函数,解题步骤如下:1、根据正弦定理将边转化为只与角C有关的式子,然后用化简后用辅助角公式合二为一,最后求出最大值及取到最大值的角C,从而判断出此时三角形的形状。
易错点
利用辅助角公式进行合二为一。
知识点
13.若2x+2y=1,则x+y的取值范围是 。
正确答案
(-∞,-2],
解析


考查方向
解题思路
本题考查采用基本不等式即可解出来。
易错点
本题考察了基本不等式,注意不等式的使用条件是一正二定三相等。
知识点
14. 已知过点



正确答案
【答案】x-3y-6=0 ,
解析
由已知可得圆的半径为5,而弦长刚好等于直径,所以直线经过圆心,由直线方程的两点式方程可以求出直线的方程为x-3y-6=0。
考查方向
解题思路
本题可以将已知条件转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去利用勾股定理算出圆心到直线的距离,然后利用点到直线的距离构造一个关于斜率的方程解出即可。
易错点
本题不知道将已知转化到弦长和半径以及圆心到直线的距离所构成的直角三角形中去求解。
知识点
16. 定义在[-2,2]上的偶函数f(x)在[-2,0]上为增,若满足f(1-m) <f(m),则m的取值范围是
正确答案
【答案】
解析
由已知再结合偶函数的性质可知在[0,2]上单调递减,所以满足

考查方向
解题思路
利用函数的奇偶性找到对称的定义域上函数的单调性,然后利用函数的单调性得到一个不等式,再结合函数的定义域,解一个不等式组即可。
易错点
本题容易忽视函数的定义域。
知识点
15.二次函数


正确答案

解析
当a=0时显然不可能,对称轴为x=-1,当a>0时,在x=2时取到最大值4,此时解得

考查方向
解题思路
分开口向上时,离对称轴远的函数值越大得到最大值在2的时候取到,当开口向下的时候在对称轴位置取到最大值,在两种情形下分别解出即可得到两个答案。
易错点
本题不知道对二次函数分开口向上和开口向下的两种情形去讨论。