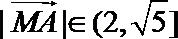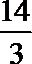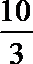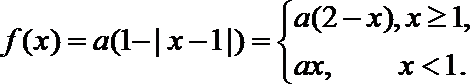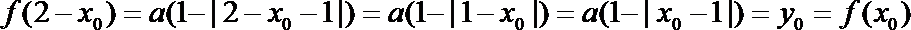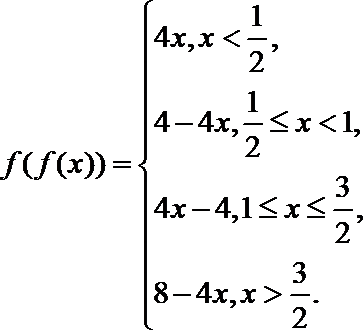- 真题试卷
- 模拟试卷
- 预测试卷
2.若抛物线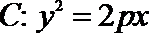
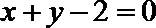
正确答案
x=-2
解析
解析已在路上飞奔,马上就到!
知识点
3.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.阅读如下图所示的程序框图,如果输入的

正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
6.已知集合

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
10.在平面上,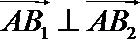
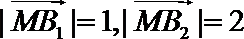
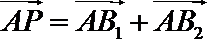
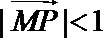
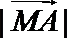
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.函数


正确答案
1/4
解析
解析已在路上飞奔,马上就到!
知识点
1.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.若

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
7.年龄在60岁(含60岁)以上的人称为老龄人,某小区的老龄人有350人, 他们的健康状况如下表:
其中健康指数的含义是:2代表“健康”,1代表“基本健康”,0代表“不健康,但生活能够自理”,-1代表“生活不能自理”.则随机访问该小区一位80岁以下的老龄人,该老人生活能够自理的概率是_____(用分数作答)。
正确答案
287/300
解析
解析已在路上飞奔,马上就到!
知识点
9.已知函数



正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
13.已知关于t的一元二次方程

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 已知向量序列:







正确答案
9;3
解析
解析已在路上飞奔,马上就到!
知识点
12.对于任意正整数,定义“n的双阶乘n!!”如下:对于n是偶数时,n!!=n·(n-2)·(n-4)……6×4×2;对于n是奇数时,n!!=n·(n-2)·(n-4)……5×3×1.
现有如下四个命题:
①(2013!!)·(2014!!)=2014!;
②2014!!=21007·1007!;
③ 2014!!的个位数是0;
④ 2015!!的个位数是5。
正确的命题是________。
正确答案
①②③④
解析
解析已在路上飞奔,马上就到!
知识点
8.平面









正确答案
直线
解析
解析已在路上飞奔,马上就到!
知识点
16.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.若直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.下列函数中周期为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
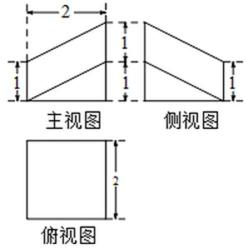
17.棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.圆形广场的有南北两个大门在中轴线上,东、西各有一栋建筑物与北门的距离分别为30米和40米,且以北门为顶点(视大门和建筑物为点)的角为
正确答案
设南、北门分别为点A、B,东、西建筑物分别为点C、D.
在△BCD中,


由于
所以
所以广场直径约为41.63米。
解析
解析已在路上飞奔,马上就到!
知识点
21.设椭圆




(1)求椭圆的方程;
(2)求线段

(3)若直线

正确答案
(1)椭圆方程为
(2)设


则

①

因
所以
即

(3)设平行于

代入椭圆方程得

△
解得

把
解得
从而解得
把
整理得 



所以
解析
解析已在路上飞奔,马上就到!
知识点
20.设底面直径和高都是4的圆柱的内切球为
(1)求球
(2)



正确答案
(1)
(2)
所以AB两点间的球面距离为
解析
解析已在路上飞奔,马上就到!
知识点
22.数列





(1)求
(2)求
(3)求
正确答案
(1)
(2)解1由(1)猜想:
用数学归纳法证明:
① 
②设
则由归纳假设得 
那么
即

即
由①、②可知,猜想成立.
解2 因
以


当


②-①得 
由

当

即
所以
(3)若
则
若
则
所以
解析
解析已在路上飞奔,马上就到!
知识点
23.已知函数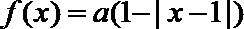
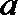
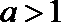
(1)求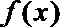
(2)证明函数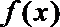
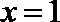
(3)当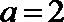
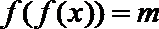
正确答案
(1)
当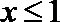
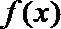
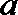
当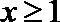
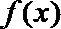
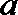
故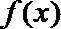
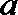
(2)设点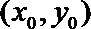
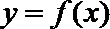
所以,函数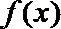
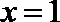
(3)当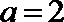
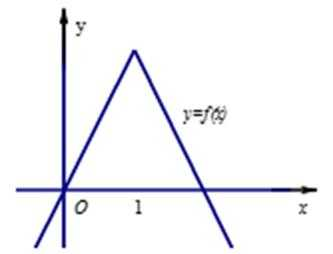
如图,
当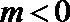
当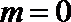
当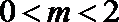
当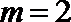
综合上述,
当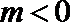
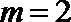
当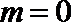
当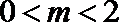
解析
解析已在路上飞奔,马上就到!