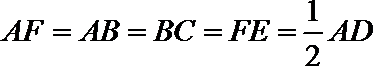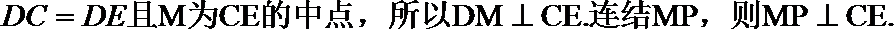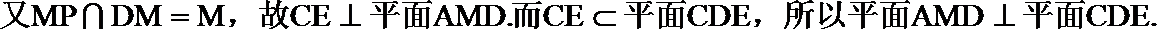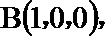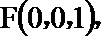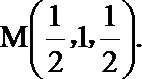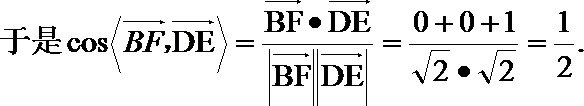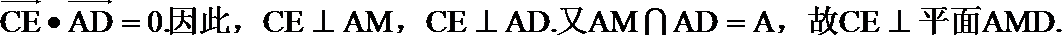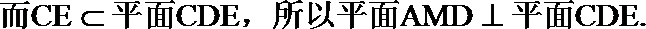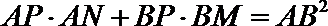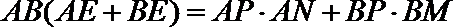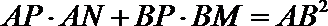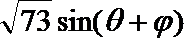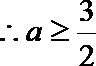- 真题试卷
- 模拟试卷
- 预测试卷
3. 命题“存在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在等差数列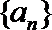
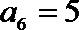
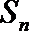
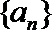
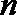
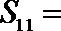
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.设抛物线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设变量x,y满足约束条件:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下图是一个算法的程序框图,该算法输出的结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知球的直径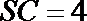
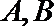
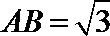
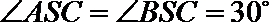
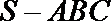
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设双曲线

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.在区间



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.有一个几何体的三视图及其尺寸如下(单位
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知关于



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在四边形



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.给出下列四个命题中:
①命题“

②“


③设圆


④关于



其中所有真命题的序号是______________。
正确答案
①,②,③,④
解析
解析已在路上飞奔,马上就到!
知识点
18.某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:
(Ⅰ)根据上面频率分布表,推出①,②,③,④处的数值分别为________,________, ________,________;
(Ⅱ)在所给的坐标系中画出区间[80,150]上的频率分布直方图;
(Ⅲ)根据题中信息估计总体:
(ⅰ)120分及以上的学生数;
(ⅱ)平均分;
(ⅲ)成绩落在[126,150]中的概率.
正确答案
解:
(Ⅰ)①,②,③,④处的数值分别为:3,0.025,0.100,1.
(Ⅱ)
(Ⅲ)(ⅰ)120分及以上的学生数为:(0.275+0.100+0.050)×5000=2125;
(ⅱ)平均分为:
(ⅲ)成绩落在[126,150]中的概率为:
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知椭圆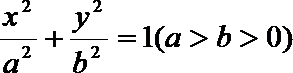
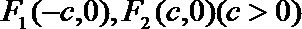
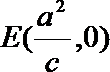
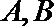
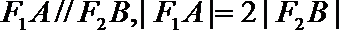
(1)求椭圆的离心率; 求直线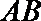
(2)设点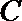
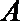
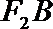
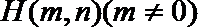
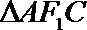

正确答案
解:(1)由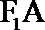
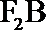
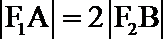
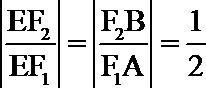
整理,得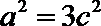
由(1)得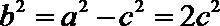
设直线AB的方程为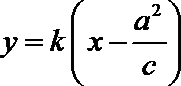
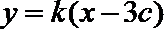
由已知设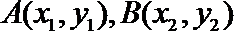
消去y整理,得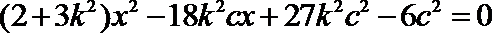
依题意,
而 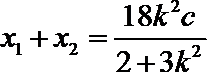
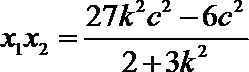
由题设知,点B为线段AE的中点,所以
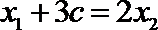
联立①③解得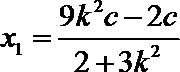
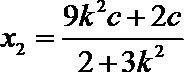
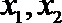
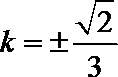
(2)解法一:可知
当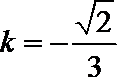
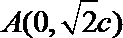
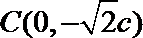
线段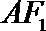
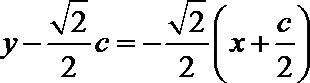
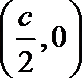
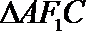
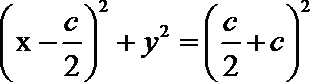
直线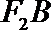
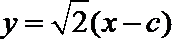
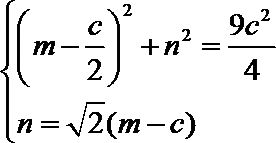
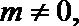
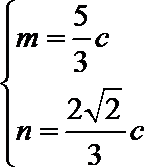
当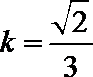
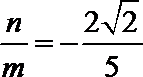
解法二:可知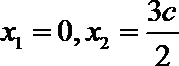
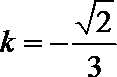
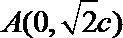
由椭圆的对称性可知B,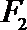
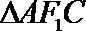
且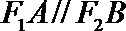
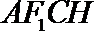
由直线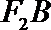
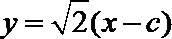
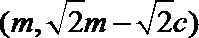
因为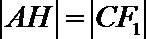
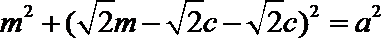
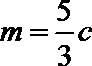
则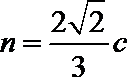
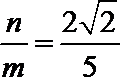
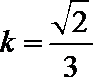
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数


(1)求a、b的值;
(2)若对于任意的

正确答案
解:(1)
因为函数




即


(2)由(1)可知,

当



当




又

则当


因为对于任意的

所以 


因此

解析
解析已在路上飞奔,马上就到!
知识点
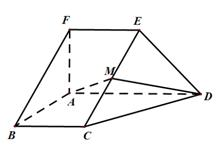
19.如图,在五面体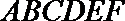
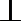
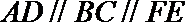
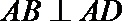
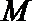
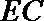
(I)求异面直线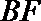
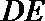
(II)证明平面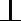
正确答案
方法一:
(Ⅰ)解:由题设知,BF//CE,所以∠CED(或其补角)为异面直线BF与DE所成的角。
设P为AD的中点,连结EP,PC。
因为FE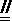

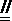
又FA⊥平面ABCD,所以EP⊥平面ABCD。
而PC,AD都在平面ABCD内,故EP⊥PC,EP⊥AD。
由AB⊥AD,可得PC⊥AD设FA=a,则EP=PC=PD=a,CD=DE=EC=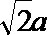
所以异面直线BF与DE所成的角的大小为60°
(II)证明:因为
方法二:建立空间直角坐标系,
点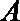
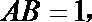
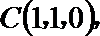
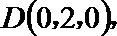
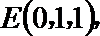
(I)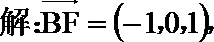
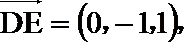
所以异面直线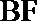
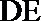
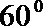
(II)证明: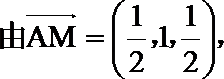
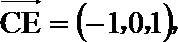
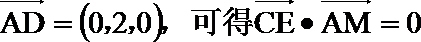
解析
解析已在路上飞奔,马上就到!
知识点
17.在


(I) 求
(II) 求
正确答案
(Ⅰ)解:在△ABC中,根据正弦定理,
(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=
于是 sinA=

所以 sin(2A-


解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答
22.选修4—1 几何证明选讲
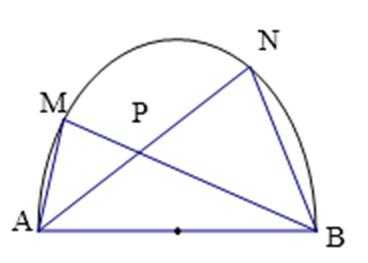
在直径是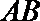
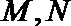
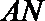
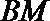
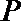
求证:
23.选修4—4 极坐标系与参数方程
已知圆方程为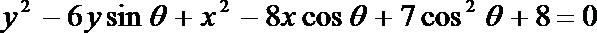
(1)求圆心轨迹的参数方程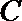
(2)点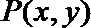
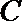
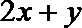
24.选修4—5 不等式选讲
(1)已知关于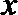
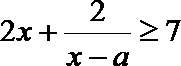
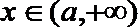
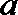
(2)已知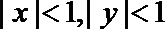

正确答案
22.
证明:作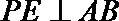
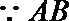
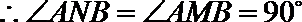
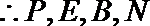
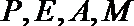
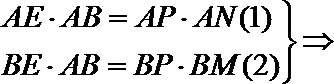
即
23.
(1)将圆的方程整理得:(x-4cos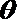
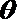
则
(2)2x+y=8cos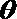
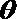
∴ -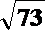
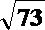
24.
(1)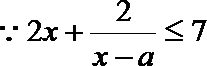
(2)因为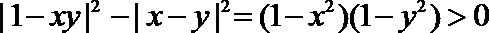
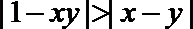
解析
解析已在路上飞奔,马上就到!