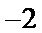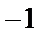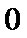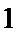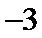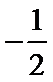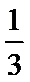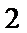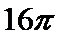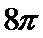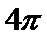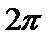- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合



正确答案
解析
由



考查方向
解题思路
先分别求出两个集合中代表元素的取值范围,再求交集。
易错点
集合Q中不等式解错导致出错。
知识点
2.已知




正确答案
解析
由


考查方向
解题思路
先求出复数z,再利用共轭复数的概念即可求出其共轭复数。
易错点
求复数Z时容易出错。
知识点
3.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米1534石,验得米内夹谷,抽样取米一把,数得254粒内夹谷28粒,则这批米内夹谷约为( )
正确答案
解析
样本中夹谷的比例为

考查方向
解题思路
由样本中夹谷的比例即可求出这批米内夹谷的总量。
易错点
不能准确理解题意导致出错。
知识点
4.等差数列




正确答案
解析
因为





考查方向
解题思路
由已知
易错点
对等差数列的前n项和公式不熟悉导致出错。
知识点
5.在平面直角坐标系中,
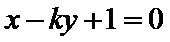
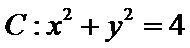
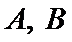
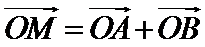
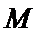
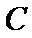
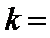
正确答案
解析
设AB中点为D,由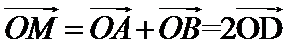
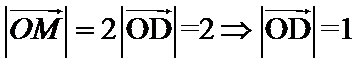
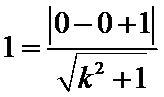
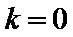
考查方向
解题思路
设AB中点为D,有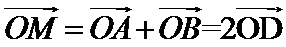
易错点
对已知条件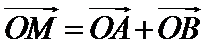
知识点
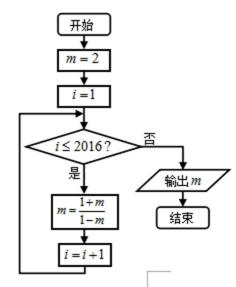
8.运行如图所示的程序框图后,输出的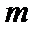
正确答案
解析
由程序框图可知,第一次循环,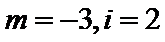
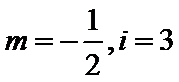
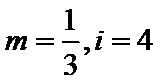
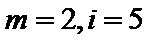
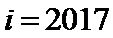
考查方向
解题思路
根据条件确定求出周期,即可求出循环结束时输出m的值。
易错点
不知何时终止循环导致出错。
知识点
9.如图,一个摩天轮的半径为18m,12分钟旋转一周,它的最低点P0离地面2m,∠P0OP1=15º,摩天轮上的一个点P从P1开始按逆时针方向旋转,则点P离地面距离y(m)与时间x(分钟)之间的函数关系式是( )
正确答案
解析
设函数关系式为






考查方向
解题思路
根据题意建立模型,再利用三角函数的性质即可求出解析式。
易错点
不能准确建立模型导致出错。
知识点
6.某空间几何体的三视图如图所示,则此几何体的体积是( )
正确答案
解析
由三视图可知该几何体的直观图是四棱锥

考查方向
解题思路
由三视图可知该几何体的直观图如右图所示,则多面体的体积可求出。
易错点
不能将三视图还原为原图导致出错。
知识点
7.若x,y满足约束条件

正确答案
解析
画出不等式组




考查方向
解题思路
根据约束条件画出可行域,作出直线
易错点
不知道目标函数的几何意义导致本题出错。
知识点
10.已知函数



若函数


正确答案
解析
由题意得:当





考查方向
解题思路
先根据奇偶性求出函数的解析式,再利用单调性求出参数的范围。
易错点
不知如何判断分段函数的单调性导致本题出错。
知识点
12.若函数

正确答案
解析
由题意得:














考查方向
解题思路
先求导,由导数与极值的关系求出参数的范围。
易错点
不知导数与极值的关系导致本题出错。
知识点
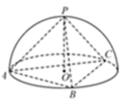
11.正三棱锥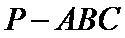
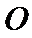
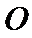
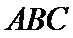
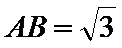
表面积为( )
正确答案
解析
如下图所示,由题意得球心O为等边三角形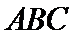
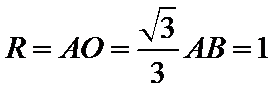
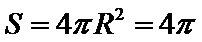
考查方向
解题思路
先根据题意求出半径,再利用球的表面积公式求球的表面积。
易错点
不知如何建立模型求球的半径导致本题出错。
知识点
15.平面向量






小值是 .
正确答案
解析
试题分析:依题意可知




考查方向
解题思路
对
易错点
相关知识点不熟悉导致出错。
知识点
16.已知



线的左右两支分别交于

为 .
正确答案
解析
试题分析:依题意做出图像,如下图所示,根据双曲线的定义得





考查方向
解题思路
直接利用双曲线的定义及几何性质进行运算。
易错点
相关知识点不熟悉导致出错。
知识点
13.若

正确答案
解析
试题分析:依题意可知


考查方向
解题思路
直接运用倍角公式及诱导公式即可求解。
易错点
相关知识点不熟悉导致出错。
知识点
14.各项均为正数的等比数列



正确答案
解析
试题分析:由




考查方向
解题思路
直接利用等比数列的通项公式进行计算。
易错点
相关知识点不熟悉导致出错。
知识点
在四棱锥






21.证明:
22.在线段



正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
由PA⊥平面ABCD,得DE⊥PA.连接AE,因为
考查方向
解题思路
利用相关定理进行证明.
易错点
相关定理不熟容易处错。
正确答案
见解析
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:过点F作FH∥ED交AD于点H,则FH∥平面PED,且有AH=

由面面平行的判定定理可得平面GEH∥平面PFD.,进而由面面平行的性质得到EG∥平面PFD,从而确定G点位置.
考查方向
解题思路
假设平行,利用平行确定点的位置.
易错点
相关定理不熟容易处错。
PM2.5是指空气中直径小于或等于2.5微米的颗粒物,为了探究车流辆与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的浓度的数据如下表:
19.根据上表数据,用最小二乘法求出

20.若周六同一时间段车流量是200万辆,试根据19题中求出的线性回归方程预测,此时PM2.5的浓度是多少?
附:线性回归方程




正确答案

解析
试题分析:本题属于最小二乘法、回归直线方程的求法、线性回归分析,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:






故


考查方向
解题思路
直接利用公式进行计算;
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于最小二乘法、回归直线方程的求法、线性回归分析,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:当


考查方向
解题思路
根据回归直线方程进行估计.
易错点
相关知识点不熟容易处错。
已知中心在坐标原点,焦点在





23.求椭圆
24.若







正确答案

解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:由题意知






考查方向
解题思路
利用相关知识求椭圆方程;
易错点
对题中条件的处理容易出错。
正确答案

解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:设









因为


整理得
所以





考查方向
解题思路
联立方程组,利用题中所给条件找关系,整理即可求解.
易错点
对题中条件的处理容易出错。
在△



17.若

18.若

正确答案

解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
因为



因为


因此
考查方向
解题思路
直接利用正弦定理及边角关系进行计算;
易错点
相关知识点不熟容易处错。
正确答案

解析
试题分析:本题属于正余弦定理的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
设



考查方向
解题思路
设


易错点
相关知识点不熟容易处错。
已知函数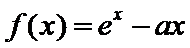
25.当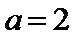
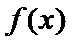
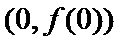
26.在25题的条件下,求证: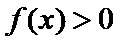
27.当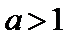
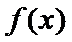
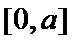
正确答案
见解析
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
当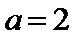
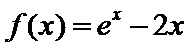
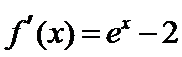
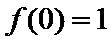
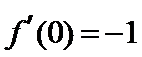
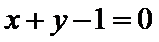
考查方向
解题思路
利用导数的几何意义求切线方程;
易错点
第三问对题中所给条件不知如何下手导致失分。
正确答案
见解析
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
由25题知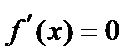

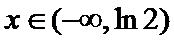
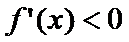

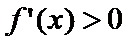
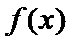
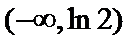
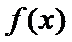
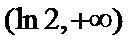
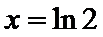
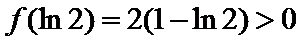
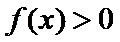
考查方向
解题思路
利用单调性进行证明;
易错点
第三问对题中所给条件不知如何下手导致失分。
正确答案
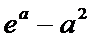
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:
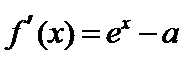
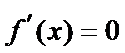
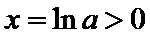
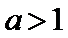
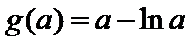
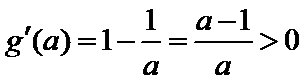
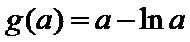
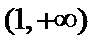

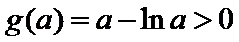
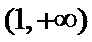
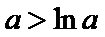
当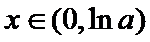
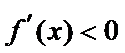
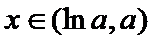
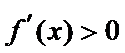
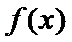
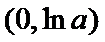
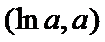
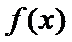
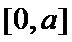
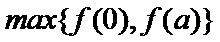
因为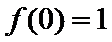

设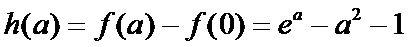
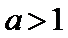
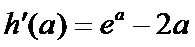
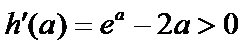
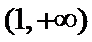
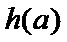
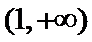
又因为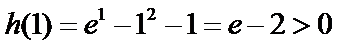
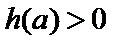
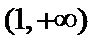
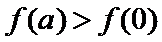
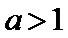
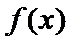

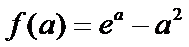
考查方向
解题思路
利用函数的单调性求最值.
易错点
第三问对题中所给条件不知如何下手导致失分。
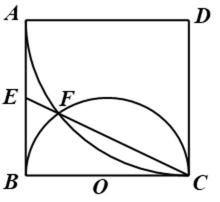
选修4—1:几何证明选讲
如图,正方形
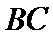
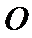

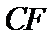
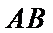
28.求证: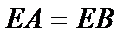
29.求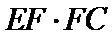
正确答案
见解析.
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下: 由以D为圆心DA为半径作圆,而ABCD为正方形,所以EA为圆D的切线.得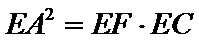
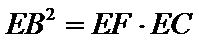
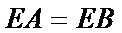
考查方向
解题思路
直接利用相交弦定理即可证明.
易错点
不熟悉射影定理导致本题失分。
正确答案

解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:连结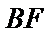
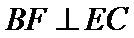
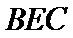
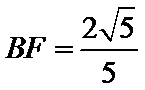

考查方向
解题思路
利用相射影定理求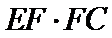
易错点
不熟悉射影定理导致本题失分。