- 真题试卷
- 模拟试卷
- 预测试卷
1.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.如图,是2008年底CCTV举办的全国钢
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.将函数

( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.设变量
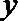
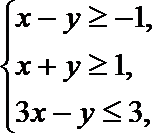
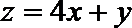
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.等差数列






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设

①
②
③
④
其中正确命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知F1 ,F2分别是双曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.曲线
正确答案
(
解析
解析已在路上飞奔,马上就到!
知识点
13.观察5000个新生婴儿的体重,其频率分布直方图如图所示,则其中新生婴儿的体重在[2700,3000]的人数为_____________。
正确答案
1500
解析
解析已在路上飞奔,马上就到!
知识点
16.图2中实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1

正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数
(1)若


(2)将函数f(x)的图像向右平移m个单位,使平移后

正确答案
(1)
f(x)
(2)
∴把


故m=
解析
解析已在路上飞奔,马上就到!
知识点
18.


(I)求函数
(II)求使两个不同向量

正确答案
设点
(Ⅰ)记

即

(Ⅱ)记两个不同向量



解析
解析已在路上飞奔,马上就到!
知识点
19.已知

(1)求数列
(2)证明
正确答案
(1)
(2)由(1)知
解析
解析已在路上飞奔,马上就到!
知识点
20.已知四棱锥


(Ⅰ)求四棱锥
(Ⅱ)若



(Ⅲ)试证:不论点

正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆

(Ⅰ)求椭圆C的方程;
(Ⅱ)已知直线


正确答案
(Ⅰ)


曲线过

由①②解得
则椭圆方程为
(Ⅱ)联立方程

则
解得


即
又∵

解得,
由③④得:
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数


(1)求

(2)若

(3)若方程



正确答案
(1)


∴

解得

(2)
(3)

则



在



当


则方程

即
解析
解析已在路上飞奔,马上就到!





























































