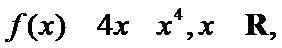- 真题试卷
- 模拟试卷
- 预测试卷
1.已知全集



正确答案
解析



考查方向
解题思路
解决此类问题一般要把参与运算的集合化为最简形式再进行运算,如果是不等式解集、函数定义域及值域有关数集之间的运算,常借助数轴进行运算.
易错点
补集的求解
知识点
3.阅读下边的程序框图,运行相应的程序,则输出i的值为( )
正确答案
解析
由程序框图可知:
考查方向
本题主要考查程序框图及学生分析问题解决问题的能力
解题思路
卷程序框图常以客观题形式出现,属于基础题,解决此类问题的关键是确定循环次数,当循环次数不多时,可以逐次列出计算结果,天津卷2014年第3题和本题是同一类问题,希望考生留意这种命题方式.
知识点
2.设变量


正确答案
解析
作出不等式组对应的平面区域如图:(阴影部分).由z=3x+y得y=-3x+z,平移直线y=-3x+z,由图象可知当直线y=-3x+z经过点A时,直线y=-3x+z的截距最大,此时z最大.,当 
考查方向
解题思路
线性规划也是高考中常考的知识点,一般以客观题形式出现,基本题型是给出约束条件求目标函数的最值,常见的结合方式有:纵截距、斜率、两点间的距离、点到直线的距离,解决此类问题常利用数形结合,准确作出图形是解决问题的关键
易错点
根据题意正确作出约束条件对应的平面区域图象.
知识点
5.已知双曲线


正确答案
解析
由双曲线的渐近线




考查方向
解题思路
本题是圆与双曲线的交汇题,虽有一定的综合性,但方法容易想到,仍属于基础题.不过要注意解析几何问题中最容易出现运算错误,所以解题时一定要注意运算的准确性与技巧性,基础题失分过多是相当一部分学生数学考不好的主要原因
易错点
点到直线的距离公式的运用
知识点
4.设


正确答案
解析
由


考查方向
解题思路
本题考查的知识点有两个,一是绝对值不等式的解法,与本题有关的结论是:若






易错点
对于非空集合




知识点
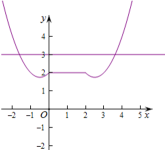
7.已知定义在R上的函数


正确答案
解析
由




考查方向
解题思路
函数是高考中的重点与热点,客观题中也会出现较难的题,解决此类问题要充分利用相关结论.函数


易错点
函数单调性的正确运用
知识点
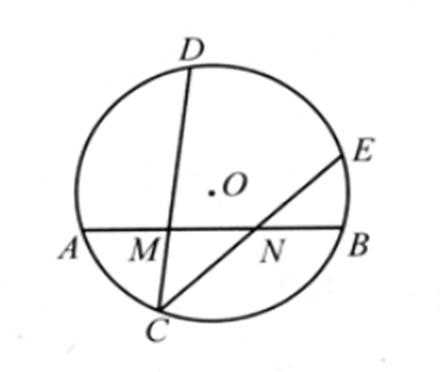
6.如图,在圆O中,M,N是弦AB的三等分点,弦CD,CE分别经过点M,N,若CM=2,MD=4,CN=3,则线段NE的长为( )
正确答案
解析
根据相交弦定理可得 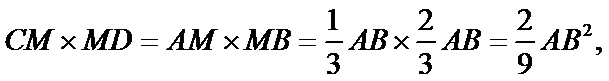
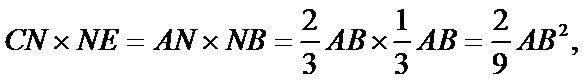
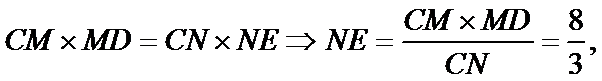
考查方向
解题思路
平面几何中与圆有关的性质与定理是高考考查的热点,解题时要充分利用性质与定理求解,本部分内容中常见的命题点有:平行线分线段成比例定理;三角形的相似与性质;圆内接四边形的性质与判定;相交弦定理与切割线定理.
易错点
相交弦定理的灵活运用
知识点
8.已知函数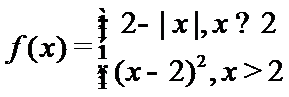
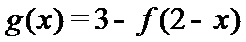
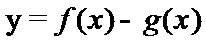
正确答案
解析
当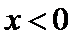
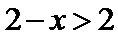
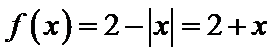
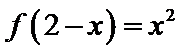
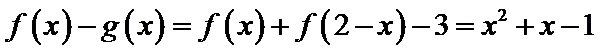
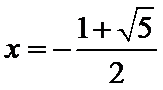
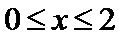
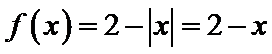
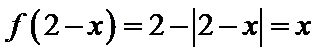
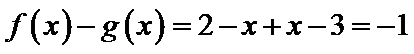
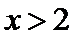
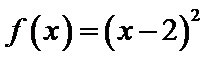
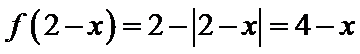
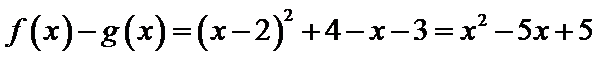
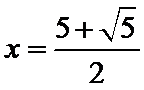
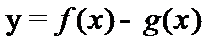
考查方向
解题思路
本题解法采用了直接解方程求零点的方法,这种方法对运算能力要求较高.含有绝对值的分段函数问题,一直是天津高考数学试卷中的热点,这类问题大多要用到数形结合思想与分类讨论思想,注意在分类时要做到:互斥、无漏、最简.
易错点
正确进行分类讨论
知识点
9.i是虚数单位,计算
正确答案
-i
解析

考查方向
解题思路
复数题也是每年高考必考内容,一复数般以客观题形式出现,属得分题.高考中复数考查频率较高的内容有:复数的几何意义,共轭复数,复数的模及复数的乘除运算,这类问题一般难度不大,但容易出现运算错误,特别是
易错点
复数的运算性质
知识点
11.已知函数



正确答案
3
解析
因为

考查方向
解题思路
本题考查内容单一,求出

易错点
导数的运算
知识点
12.已知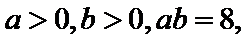
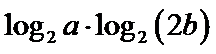
正确答案
4
解析
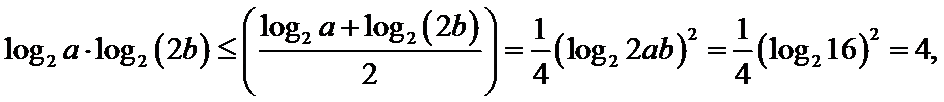
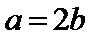
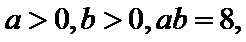
考查方向
解题思路
在利用基本不等式求最值时,一定要紧扣“一正、二定、三相等”这三个条件,注意创造“定”这个条件时常要对所给式子进行拆分、组合、添加系数等处理,使之可用基本不等式来解决,若多次使用基本不等式,必须保持每次取等的一致性.
易错点
不等式取等号的条件
知识点
13.在等腰梯形ABCD中,已知



正确答案
解析
在等腰梯形ABCD中,由




考查方向
解题思路
高考对平面向量数量积的考查主要是向量的模,夹角的运算及平行与垂直的判断与应用,在利用数量积的定义进行计算时,要善于将相关向量分解为图形中模与夹角已知的向量进行运算,运算时一定要注意向量的方向,搞清两向量的夹角.
易错点
向量的长度与夹角的计算
知识点
10.一个几何体的三视图如图所示(单位:m),则该几何体的体积为 
正确答案
解析
该几何体是由两个高为1的圆锥与一个高为2的圆柱组合而成,所以该几何体的体积为
考查方向
解题思路
由于三视图能有效的考查学生的空间想象能力,所以以三视图为载体的立体几何题基本上是高考每年必考内容,高考试题中三视图一般常与几何体的表面积与体积交汇.由三视图还原出原几何体,是解决此类问题的关键.
易错点
根据三视图得到组合体的空间结构
知识点
14.已知函数






正确答案
解析
由





考查方向
解题思路
本题将三角函数单调性与对称性结合在一起进行考查,叙述方式新颖,是一道考查能力的好题.注意本题解法中用到的两个结论:①




易错点
函数性质的灵活运用
知识点
如图,已知





19.求证:EF∥平面
20.求证:平面

21.求直线

正确答案
要证明EF∥平面

证明:如图,连接





解析
见答案.
考查方向
易错点
线面关系与面面关系的转化
正确答案
要证明平面



因为AB=AC,E为BC中点,所以










解析
见答案.
考查方向
易错点
线面垂直于面面垂直的转化.
正确答案

解析
取









取

























考查方向
易错点
线面角定义的灵活运用
已知椭圆


24.求直线BF的斜率;
25.设直线BF与椭圆交于点P(P异于点B),过点B且垂直于BP的直线与椭圆交于点Q(Q异于点B)直线PQ与y轴交于点M,
(i)求
(ii)若
正确答案
2.
解析
试题分析:先由



设






考查方向
解题思路
高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试内容,主要由求值、求方程、求定值、最值、求参数取值范围等几部分组成,其中考查较多的圆锥曲线是椭圆,解决这类问题要重视方程思想、函数思想及化归思想的应用.
易错点
椭圆几何性质的理解运用
正确答案
(i)
解析
试题分析:(i)先把直线BF,BQ的方程与椭圆方程联立,求出点P,Q横坐标,可得



设点










(ii)由(i)得





又因为


考查方向
解题思路
高考解析几何解答题大多考查直线与圆锥曲线的位置关系,直线与圆锥曲线的位置关系是一个很宽泛的考试内容,主要由求值、求方程、求定值、最值、求参数取值范围等几部分组成,其中考查较多的圆锥曲线是椭圆,解决这类问题要重视方程思想、函数思想及化归思想的应用.
易错点
;韦达定理的正确运用及正确化简计算
设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
15.求应从这三个协会中分别抽取的运动员人数;
16.将抽取的6名运动员进行编号,编号分别为
(i)用所给编号列出所有可能的结果;
(ii)设A为事件“编号为
正确答案
3,1,2
解析
试题分析:由分层抽样方法可知应从甲、乙、丙这三个协会中分别抽取的运动员人数分别为3,1,2.
考查方向
解题思路
注意分层抽样是按比例抽取
易错点
抽取比例的确定
正确答案
(i)见试题解析;(ii)
解析
试题分析:(i)一一列举,共15种;(ii)符合条件的结果有9种,所以
(II)(i)从这6名运动员中随机抽取2名参加双打比赛,所有可能的结果为














(ii)编号为









考查方向
解题思路
求古典概型的概率关键是求m与n的值,常借助表格、树状图、以及列举法进行计算,注意基本事件的列举要按照一定的顺序进行列举,否则,容易出现遗漏或重复的现象,这点要引起考生重视..
易错点
准确列举基本事件,准确找到满足条件的事件
△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为
17.求a和sinC的值;
18.求
正确答案
a=8,
解析
试题分析:由面积公式可得


△ABC中,由








考查方向
解题思路
解三角形问题实质是附加条件的三角变换,因此在解三角形问题的处理中,正弦定理、余弦定理就起到了适时、适度转化边角的作用,分析近几年的高考试卷,有关的三角题,大部分以三角形为载体考查三角变换.
易错点
三角形面积公式的运用及边角关系的互化
正确答案

解析
试题分析:(II)直接展开求值.

考查方向
解题思路
解三角形问题实质是附加条件的三角变换,分析近几年的高考试卷,有关的三角题,大部分以三角形为载体考查三角变换.
易错点
和角公式的正确运用
已知



22.求

23.设

正确答案


解析
试题分析:列出关于q与d的方程组,通过解方程组求出q,d,即可确定通项;设









考查方向
解题思路
近几年高考试题中求数列通项的题目频频出现,尤其对等差、等比数列的通项考查较多,解决此类 问题要重视方程思想的应用.
易错点
准确求解方程
正确答案
解析
试题分析:用错位相减法求和.
由(I)有


两式相减得
所以
考查方向
解题思路
错位相减法求和也是高考考查频率较高的一类方法,从历年考试情况来看,这类问题,运算失误较多,应引起考生重视.
易错点
错位相减法相减时项的对应关系
已知函数
26.求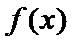
27.设曲线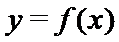
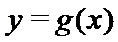
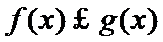
28.若方程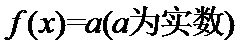
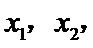
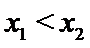
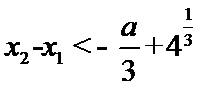
正确答案
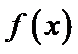
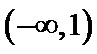
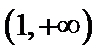
解析
试题分析:由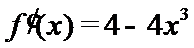
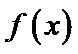
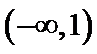
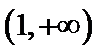
由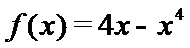
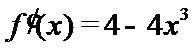
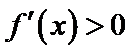
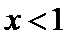
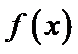
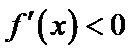
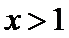
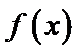
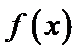
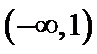
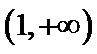
考查方向
解题思路
给出可导函数求单调区间,实质是解关于导函数的不等式,若函数解析式中不含参数,一般比较容易.不过要注意求单调区间,要注意定义域优先原则,且结果必须写成区间形式,不能写成不等式形式.
易错点
导数函数性质与原函数单调性的关系.
正确答案
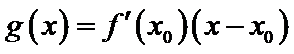
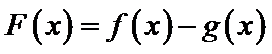
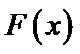
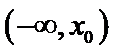
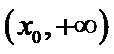
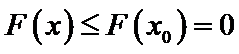
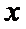
设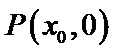
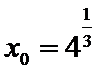
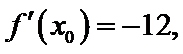
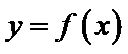
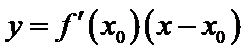
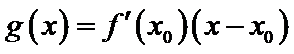
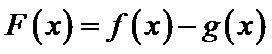
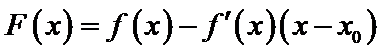
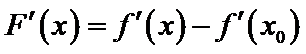
由于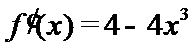
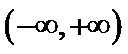
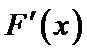
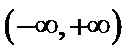
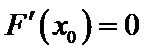
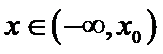
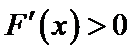
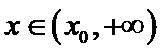
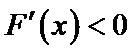
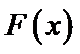
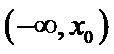
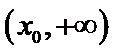
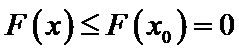
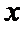
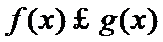
解析
见答案.
考查方向
解题思路
利用导数证明不等式是近几年高考的一个热点,解决此类问题的基本思路是构造适当的函数,利用导数研究函数的单调性和极值破解.
易错点
构造函数的性质与所求问题的联系
正确答案
设方程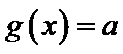
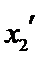
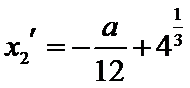
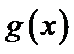
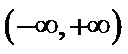
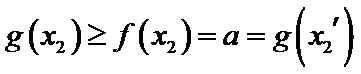
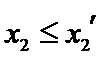
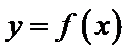
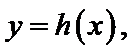
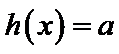
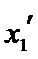
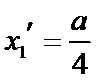
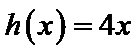
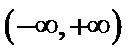
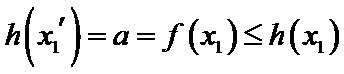
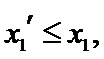
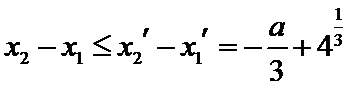
由(II)知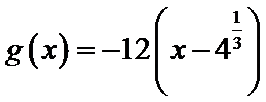
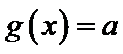
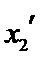
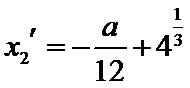
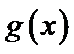
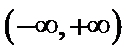
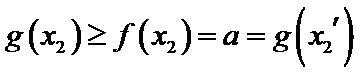
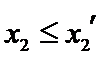
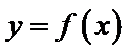
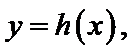
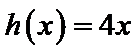
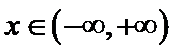
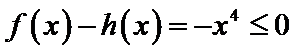
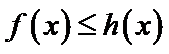
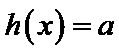
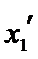
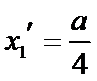
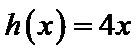
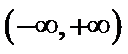
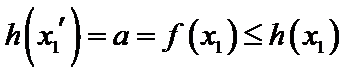
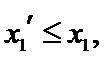
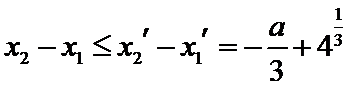
解析
见答案.
考查方向
解题思路
利用导数证明不等式是近几年高考的一个热点,解决此类问题的基本思路是构造适当的函数,利用导数研究函数的单调性和极值破解.
易错点
导数的几何意义及导函数与原函数之间的联系