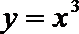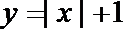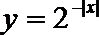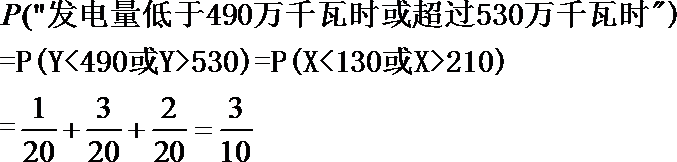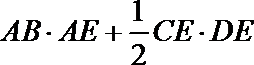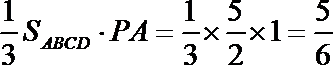- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合U={1, 2,3,4,5},A={1,3,5},B={2,5},则A∩(CUB)等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下列函数中既是偶函数又在(0,+∞)上是增函数的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若点(a,9)在函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某校选修乒乓球课程的学生中,高一年级有30名,高二年级有40名。现用分层抽样的方法在这70名学生中抽取一个样本,已知在高一年级的学生中抽取了6名,则在高二年级的学生中应抽取的人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知向量a=(2,1),b=(-1,k),a·(2a-b)=0,则k=( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若a>0,b>0,且函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数f(x)的定义域为R,f(-1)=2,对任意


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
(
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数f(x)是一次函数,且满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知x和y是实数,且满足约束条件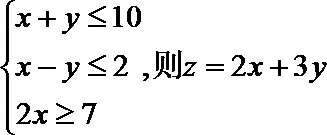
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知




正确答案
45°
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数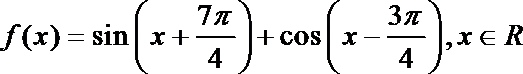


正确答案
=

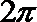
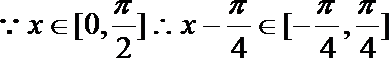
函数取得最小值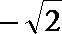
解析
解析已在路上飞奔,马上就到!
知识点
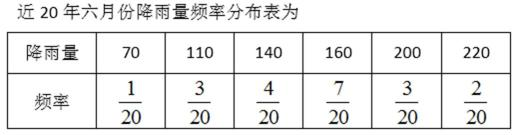
20.某河流上的一座水力发电站,每年六月份的发电量Y(单位:万千瓦时)与该河上游在六月份的降雨量X(单位:毫米)有关。据统计,当X=70时,Y=460;X每增加10,Y增加5;已知近20年X的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(1)完成如下的频率分布表:
(2)假定今年六月份的降雨量与近20年六月份的降雨量的分布规律相同,并将频率视为概率,求今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率。
正确答案
(1)在所给数据中,降雨量为110毫米的有3个,
为160毫米的有7个,为200毫米的有3个,故
(2)
故今年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率为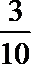
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,直线l :y=x+b与抛物线C :x2=4y相切于点A。
(1)求实数b的值;
(2)求以点A为圆心,且与抛物线C的准线相切的圆的方程。
正确答案
(1)由


因为直线与抛物线C相切
所以
解得
(2)由(1)可知
故方程(
解得
得y=1
故点A(2,1)
因为圆A与抛物线C的准线相切
所以圆心A到抛物线C的准线y=-1的距离等于圆A的半径r
即r=|1-(-1)|=2
所以圆A的方程为
解析
解析已在路上飞奔,马上就到!
知识点
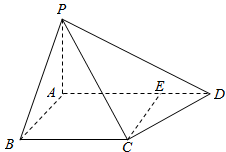
19.如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
(1)求证:CE⊥平面PAD;
(2)若PA=AB=1,AD=3,CD=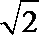
正确答案
(1)证明:因为PA⊥平面ABCD,CE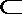
所以PA⊥CE,
因为AB⊥AD,CE∥AB,
所以CE⊥AD,
又PA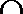
所以CE⊥平面PAD
(2)解:由(1)可知CE⊥AD,在直角三角形ECD中,
DE=CD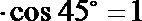
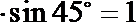
又因为AB=CE=1,AB∥CE,
所以四边形ABCE为矩形,
所以
=
=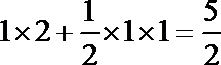
又PA⊥平面ABCD,PA=1,
所以四棱锥P-ABCD的体积等于
解析
解析已在路上飞奔,马上就到!
知识点
21.在数列

(1)求数列
(2)求证:数列
(3)设数列



正确答案
(1)∵
∴数列{


∴
(2)∵
∴
∴
∴数列


(3)由(1)知,


∴
∴
于是
两式①-②相减得
=
∴
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(1)求
(2)求

正确答案
(1)
令
所以


(2)当
函数

所以
当

由(1)知
函数


所以
当
函数

所以
解析
解析已在路上飞奔,马上就到!