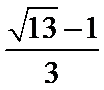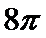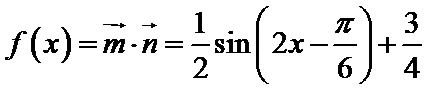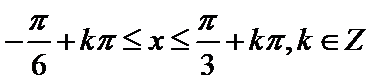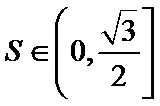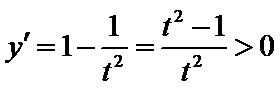- 真题试卷
- 模拟试卷
- 预测试卷
2.若
A
B
C
D
正确答案
解析
考查方向
解题思路
分母实数化，同时乘以分母的共轭复数化简即可。
易错点
分母不知道怎么实数化。
知识点
3.某校高三年级共有学生900人，编号为1,2,3，……，900，现用系统抽样的方法抽取一个容量为45的样本，则抽取的45人中，编号落在区间
正确答案
解析
抽样比是20，然后在要求的区间上的人数为240/20=12人，所以选C。
【修改点】增加了区间
考查方向
解题思路
先算出抽样比，在算出要求的区间所占的人数。
易错点
不理解系统抽样的概念。
知识点
4. 已知实数
A-6
B1
C3
D6
正确答案
解析
如图所示，当直线经过点（0，-1）时取得最小值1。
考查方向
解题思路
根据线性约束条件画出可行域，在平移直线找到取最值的点。
易错点
不知道在哪个位置取到最值。
知识点
8.执行右面的程序框图，则输入的
A
B
C
D
正确答案
解析
考查方向
解题思路
根据判断框的条件循环直到跳出循环，然后用数列里面的裂项相消法求和。
易错点
不知道什么时候跳出循环。
知识点
9. 已知抛物线
A
B
C
D
正确答案
解析
设M（x，y），由题意可知x+p/2=2p，所以x=3p/2，则
考查方向
解题思路
根据到焦点的距离等于到准线的距离可以将点M的坐标求出从而进一步求出MF的斜率。
易错点
不知道将到焦点的距离转化到准线的距离。
知识点
1.若集合
A
B
C
D
正确答案
解析
考查方向
解题思路
先解出集合A,然后求出两个集合的交集。
易错点
不等式的解集写反。
知识点
5. 已知不共线的两个向量
A
B2
C
D4
正确答案
解析
将已知的2个式子左右同时平方再相减即可得
【修改点】将已知
考查方向
解题思路
由垂直数量积为0得一个式子，由已知的模左右同时平方得一个式子，两式联立即可解出。
易错点
模的计算方法不清楚。
知识点
6.某中学有3个社团，每位同学参加各个社团的可能性相同，甲、乙两位同学均参加其中一个社团，则这两位同学参加不同社团的概率为（ ）
A
B
C
D
正确答案
解析
两个同学参加相同社团的概率为p=3/9=1/3,则所求事件的概率为1-1/3=2/3.
考查方向
解题思路
正难则反，可以先求出对立事件的概率，再用1减去这个概率值即可。
易错点
在找要求的事件个数容易漏解。
知识点
7. 已知等比数列
A
B
C
D
正确答案
解析
由
考查方向
解题思路
由
易错点
公比的正负情况不知道。
知识点
10. 由棱锥和棱柱组成的几何体的三视图如图所示，则该几何体的体积为（ ）
A14
B
C22
D
正确答案
解析
如图所示，几何体是由一个三棱锥和一个三棱柱组合形成的一个组合体，所以其体积为14
考查方向
解题思路
由三视图还原出直观图再来求其体积。
易错点
不知道直观图是一个什么图形。
知识点
11. 双曲线
A
B
C
D
正确答案
解析
如下图所示，根据双曲线的定义，满足
考查方向
解题思路
根据已知条件画出图像再找到关系之后可以解出。
易错点
不会将已知条件转化为所学的知识来解答。
知识点
12.定义在
A
B
C
D
正确答案
解析
过构造函数最后通过函数的奇偶性和单调性判断使
考查方向
解题思路
通过构造函数最后通过函数的奇偶性和单调性来解答。
易错点
不知道通过函数的性质以及构造函数来解答。
知识点
16.在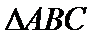
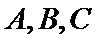
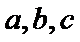
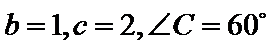
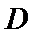
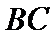
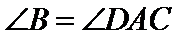
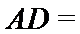
正确答案
解析
在三角形ABC中由正弦定理可以求出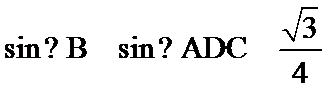
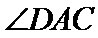
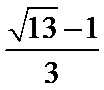
考查方向
解题思路
本题考查正余弦定理解三角形的能力，解题步骤如下：先用正弦定理求出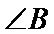
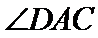
易错点
不会灵和应用定理解答。
知识点
13.若函数 
正确答案
1
解析
考查方向
解题思路
本题考查分段函数求函数值的能力，解题步骤如下：先求f（5），再继续下去直到求出其值。
易错点
带错解析式。
知识点
14.已知球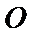
正确答案
解析
求出球的半径为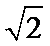
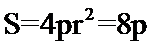
考查方向
解题思路
本题考查空间想象能力，解题步骤如下：先求球的半径再求出其表面积。
易错点
根据已知将球的半径求错。
知识点
15.已知数列
正确答案
解析
考查方向
解题思路
本题考查转化思想的能力，解题步骤如下：将
易错点
不会转化成关于和有关的式子。
知识点
17.已知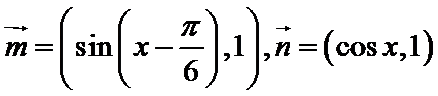
（1）若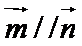
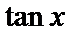
（2）若函数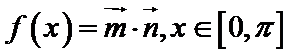
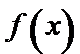
正确答案
（1）
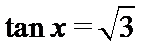
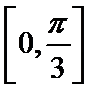
解析
试题分析：本题属于向量结合三角函数的问题，题目的难度是逐渐由易到难，
（1）直向量共线的坐标表示可以解出，
（2）先将函数求出来再化简最终可以得到单调增区间。
（1）由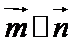
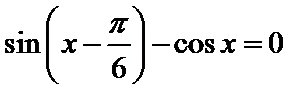
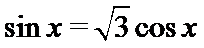
即
（2）
由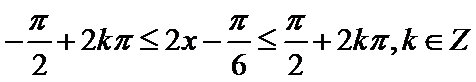
又因为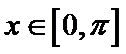
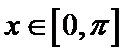
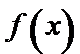
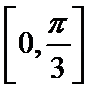
考查方向
解题思路
本题考查向量和三角函数的综合应用，解题步骤如下：由向量共线的坐标表示可以解出第一问，第二问先将函数求出来再化简最终可以得到单调增区间。
易错点
不知道怎么化简。
知识点
18.某品牌手机厂商推出新款的旗舰机型，并在某地区跟踪调查得到这款手机上市时间（
（1）根据上表中的数据，用最小二乘法求出
（2）根据上述回归方程，分析该款旗舰机型市场占有率的变化趋势，并预测自上市起经过多少个月，该款旗舰机型市场占有率能超过
附：
正确答案
（1）见下面解析；（2）13个月。
解析
试题分析：本题属于线性回归方程，
（1）直接按照步骤来求；
（2）由第一问计算出来的线性回归方程然后直接利用即可解出来。
由
预计上市13个月时，市场占有率能超过
考查方向
解题思路
本题考查线性回归方程，解题步骤如下：
（1）直接按照步骤来求；
（2）由第一问计算出来的线性回归方程然后直接利用即可解出来。
易错点
求解回归方程时候容易计算出错。
知识点
19.如图，
（1）求证：
（2）求四棱锥
正确答案
（1）见解析；（2）
解析
试题分析：本题属于立体几何中的证明和求表面积问题，
（1）线线垂直转化为由线面垂直来证明；
（2）将每个面的面积算出来，最后相加即可。
（1）取
因为
所以
因此，
（2）设四棱锥
由于
所以
所以
综上，
考查方向
解题思路
本题考查立体几何的问题，解题步骤如下：（1）线线垂直转化为由线面垂直来证明；（2）将每个面的面积算出来，最后相加即可。
易错点
不会将线线垂直转化为由线面垂直来证明。
知识点
20.已知中心在原点，焦点在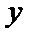
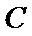
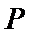
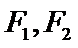
（1）求椭圆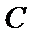
（2）若直线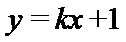
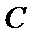
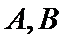
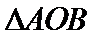
正确答案
（1）
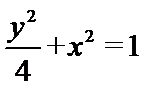
解析
试题分析：本题属于直线和椭圆位置关系的基本问题，题目的难度是逐渐由易到难，
（1）根据已知条件构造方程组；
（2）用设而不求的方法将面积表示成关于斜率的表达式，然后换元求出面积的取值范围。
（1）设椭圆的标准方程为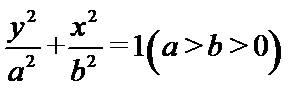
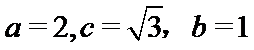
所以椭圆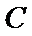
（2）设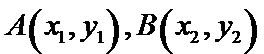
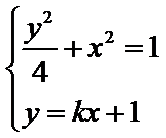
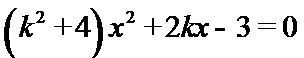
故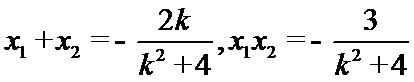
设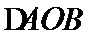
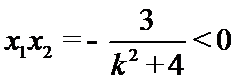
令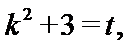
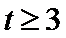
对函数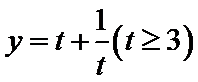
因此函数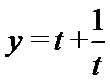
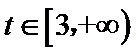
因此，
考查方向
解题思路
本题考查直线和椭圆的位置关系，解题步骤如下：
（1）根据已知条件构造方程组；
（2）用设而不求的方法将面积表示成关于斜率的表达式，然后换元求出面积的取值范围。
易错点
第二问不会用设而不求的方法来解决。
知识点
21.已知函数
（1）当
（2）设函数
正确答案
（1）
解析
试题分析：本题属于函数与导数的问题，
（1）直接按照步骤来求；
（2）求参数的范围的时候不会将其转化为求最值来解决。
（1）
设
（2）设
所以
由条件知
当
综上，
考查方向
解题思路
本题考查函数与导数，解题步骤如下：
（1）直接按照步骤来求；
（2）求参数的范围的时候不会将其转化为求最值来解决。
易错点
在求参数的范围的时候不会将转化为求最值来解决。
知识点
22.如图，
（1）求证：
（2）若
正确答案
（1）见解析；（2）
解析
试题分析：本题属于几何证明选讲的基本问题，
（1）直接按照步骤来求；
（2）由切割线定理和三角形相似即可求出。
（1）
（2）已知
得：
又知
所以
考查方向
解题思路
本题考查几何证明选讲，解题步骤如下：
（1）直接按照步骤来求；
（2）由切割线定理和三角形相似即可求出。
易错点
切割线定理不会用。