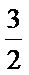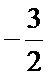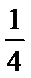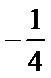- 真题试卷
- 模拟试卷
- 预测试卷
6. “

正确答案
解析
由“








综上可得,“

考查方向
本题主要考查双曲线的标准方程及充分、必要条件的概念及判定方法。
解题思路
通过



易错点
由于思维定势的影响而忽视焦点在x轴上这一重要条件,认为m,n异号即表示双曲线而出错。
知识点
7. 设

若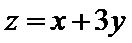
则实数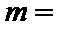
正确答案
解析
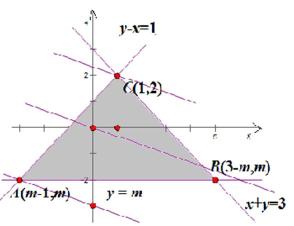
首先,作出符合题意的一个可行域如图所示(阴影部分),然后作出目标函数系方程的图像如图可知,当直线经过C(1,2)点时,Z有最大值7;当直线经过A(m-1,m)时Z有最小值:4m-1,由题意可知4m-1=0,即m=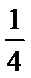
考查方向
解题思路
先假定m值作出可行域,然后作出目标函数直线系方程观测何时取最值,再利用最大值与最小值的差为7建立关于m的方程即可作答。
知识点
1.设集合



正确答案
解析
由



考查方向
解题思路
由
易错点
不理解
知识点
2. 下列函数中,值域为
正确答案
解析
由(A)




考查方向
解题思路
先由函数的值域为
易错点
不会求值域或不会判断偶函数而出错
知识点
3.设



正确答案
解析
取AB中点M,则由向量加法的平行四边形法则知


考查方向
解题思路
运用数形结合的思想解决问题,通过 
易错点
不能把
知识点
4.设命题p:“若



正确答案
解析
对于命题p:由函数




考查方向
解题思路
对于命题p:真假性的判断可利用函数的单调性辅助解决,即:构造函数

易错点
本题易在命题q:的真假性判断时忽略a,b的正负号而得出错误的结论。
知识点
5. 一个几何体的三视图如图所示,那么这个几何体的表面积是( )
正确答案
解析
由三视图可知其对应的几何体由左侧长、宽、高分别为1,2,2的长方体与右侧一侧面水平放置的三棱柱,其底面为直角边分别为1,2的直角三角形,高为2的直三棱柱
组合而成,由两个边长为2的正方形,1个长、宽分别为2,1的长方形,1个长、宽分别为2,
其表面积为:
考查方向
解题思路
首先,构建出三视图所对应的空间几何体后,然后依据其结构特征分别计算各面积之和即可。
易错点
本题易在由三视图想象其对应几何体时出错,另外在计算其表面积时组合体的结合部分面积易重复计算而出错。
知识点
8. 某市乘坐出租车的收费办法如下:
相应系统收费的程序框图如图所示,
其中

正确答案
解析
由上级判断框知,此处应该填写x>4时的收费情况,显然有
考查方向
解题思路
由图可知本题是确定x>4时收费情况的表达式即可。
易错点
本题信息量较大,从直观感觉上学生可能会由此产生畏难情绪无法深入、正确提取所需要的信息,而导致错误的产生。另一方面,不明白取整函数也可能是致错的主要原因。
知识点
10.若抛物线


正确答案

解析
由方程形式知其焦点坐标





考查方向
解题思路
由方程形式知其焦点坐标和准线方程的正确表达,把焦点坐标代入直线方程可得p的值;由此可得准线方程。
易错点
由于抛物线的标准方程有四类,相对较多学生可能由于识记问题而导致错误。
知识点
9. 已知复数


正确答案
解析

考查方向
解题思路
在等式两边同时除以

易错点
本题如若通过设Z的一般式而通过复数相等而解决由于运算量相对较大而易出错,转化为复数的除法后运算量将在一定程度上减少而减少出错。
知识点
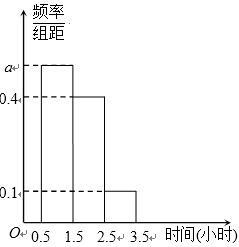
11.某校某年级有100名学生,已知这些学生完成家庭作业的时间均在区间
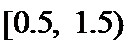
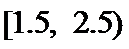
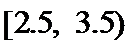
正确答案
9
解析
由分层抽样方法的特点知按3层百分之十的比例进行等比例抽取,结合如图所示的频率分布直方图.知完成作业的时间小于2.5个小时的学生占比百分之九十,即9人。
考查方向
解题思路
由分层抽样方法的特点知按3层百分之十的比例进行等比例抽取,结合如图所示的频率分布直方图.知完成作业的时间小于2.5个小时的学生占比百分之九十可得正确答案。
易错点
题目信息量相对较大,造成学生审题不清匆忙作答而出错。
知识点
13. 在





正确答案

解析
由






考查方向
解题思路
由

易错点
考查知识点相对较多,基础不扎实,对个别公式掌握不熟练而出错。
知识点
12.已知函数



正确答案
1
解析
由上面思路可知


考查方向
解题思路
由函数的图像可知:当0



易错点
不能顺利把不等式问题转化为图像的平移问题,而过份依赖由具体不等式才能解题,对于抽象函数无能为力的思维局限而无法作答出错。
知识点
14. 某食品的保鲜时间t(单位:小时)与储藏温度x(恒温,单位:



正确答案
4 是
解析
由该食品在




考查方向
解题思路
由该食品在
易错点
对于第二问不能灵活处理题目信息进行试算明确得出正确结论出错。
知识点
19.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)设动直线










正确答案
(Ⅰ)椭圆
解析
(Ⅰ)解:由题意,得

又因为点

所以
解得


所以椭圆C的方程为
(Ⅱ)证明:当直线


易得直线


当直线


由方程组

因为直线
所以

由方程组

设



所以

将
得
综上,

考查方向
解题思路
1、每一问通过椭圆离心率,点


2、第二问求证






易错点
对于第二问不考虑斜率存在与否直接解答从而导致考虑不全面而失分。
知识点
15.已知数列


(Ⅰ)求数列
(Ⅱ)设



正确答案
(Ⅰ)
解析
解:设等比数列

因为

所以
即
解得
所以
(Ⅱ)证明:因为
所以数列


所以

考查方向
解题思路
本题主要考查考等差、等比数列的概念和性质及方程思想,解题思路如下:1、由条件











易错点
本题第二问直接把数列
知识点
16.已知函数

(Ⅰ)求函数
(Ⅱ)若

正确答案
(Ⅰ)函数
(Ⅱ)

解析
本题第二问特别要注意:一定要结合函数的定义域正确书写增区间.

所以函数

(Ⅱ)解:由

得
所以函数


所以当



(注:或者写成增区间为

考查方向
解题思路
本题主要考查正、余弦的二倍角公式及
1、把

2、由

3、最后通过
易错点
本题体现了三角函数部分的基本的解题思想方法,为学生非常熟悉的题型对于第二问可能由于思维定势审题不全忽略

知识点
20.已知函数

(Ⅰ)求函数
(Ⅱ)求证:对于任意


(Ⅲ)试确定曲线

正确答案
(Ⅰ)所以函数

(Ⅲ)当





解析
(Ⅰ)解:函数

求导,得
令

当


所以函数



所以函数

(Ⅱ)证明:假设存在某个


设切点为

所以切线满足斜率

所以
即
所以假设不成立.
所以对于任意


(Ⅲ)解:“曲线


由方程

令



考察函数

因为
所以函数


而方程


所以当



故当





考查方向
解题思路
1、第一问写出函数的定义域,求出导数,然后令导数等于零解方程,列表求极值。
2、第二问直接不易证明,可考虑使用反证法:假设存在某个


3、判断曲线与直线的交点个数问题可以考虑通过函数的极值与直线的相对位置关系以及函数图像的特点采用数形结合的方法判断交点个数;也可以转化为方程判断根的个数进而确定图像交点的个数。由第一问可看出


易错点
第一问中不交待极大值不存在而失分或未考虑函数的定义域而出错;
知识点
17.如图,在四棱锥










(Ⅰ)求证:

(Ⅱ)若



(Ⅲ)当

正确答案
(Ⅲ)四棱锥
解析
(Ⅰ)证明:在平行四边形


所以
由


所以
因为侧面


所以

又因为

所以
又因为




所以

(Ⅱ)证明:因为



所以
又因为






同理,得

又因为




所以平面

又因为

所以

(Ⅲ)解:在




由

又因为
所以
因为

所以

所以四棱锥

考查方向
解题思路
1、第一问由




2、第二问可通过证明平面MEF平行平面PAB得出




3、由PA垂直平面ABCD为基础,通过作PA平行线得出四棱锥






易错点
本题前两问中的证明过程要求严谨、完整,部分学生易书写的不规范、不完整而出错。
知识点
18.甲、乙两人进行射击比赛,各射击4局,每局射击10次,射击命中目标得1分,未命中目标得0分. 两人4局的得分情况如下:
(Ⅰ)已知在乙的4局比赛中随机选取1局时,此局得分小于6分的概率不为零,且在4局比赛中,乙的平均得分高于甲的平均得分,求
(Ⅱ)如果




(Ⅲ)在4局比赛中,若甲、乙两人的平均得分相同,且乙的发挥更稳定,写出
正确答案
(Ⅰ)15
(Ⅱ)

(Ⅲ) 


解析
(Ⅰ)解:由题意,得

因为在乙的4局比赛中,随机选取1局,则此局得分小于6分的概率不为零,
所以
又因为

所以
所以
(Ⅱ)解:设 “从甲、乙的4局比赛中随机各选取1局,且得分满足
记甲的4局比赛为



为



则从甲、乙的4局比赛中随机各选取1局,所有可能的结果有16种, 它们是:















而事件








因此事件

(Ⅲ)解:



考查方向
解题思路
1、第一问由选取1局得分小于6分的概率不为零,可知x,y取值均为小于或等于5的自然数;结合乙的平均得分高于甲的平均得分确定的
2、第二问通过列举从甲、乙的4局比赛中随机各选取1局,所有可能的结果可以找出满足题意的事件数目,最终求出其概率。
3、第三问通过平均分相同得出

易错点
不能从题目中提取出