- 真题试卷
- 模拟试卷
- 预测试卷
4.已知x,y满足条件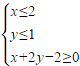
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.直线y=-2x+1 上的点到圆 x2+y2+4x-2y+4=0上的点的最近距离是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合U={1,2,3,4,5,7},集合A={4,7},集合B={1,3,4,7},则( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若a、b是空间两条不同的直线,α,β是空间的两个不同的平面,则a⊥α的一个充分不必要条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.函数y=3x+1(-1≤x<0)的反函数是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在等差数列{an}中,a1+2a8+a15=96,则2a9-a10等于( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一次演出,原计划要排4个节目,因临时有变化,拟再添加2个小品节目,若保持原有4个节目的相对顺序不变,则这6个节目不同的排列方法有( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.连接球面上两点的线段称为球的弦,半径为4的球的两条弦AB、CD的长度分别为2和4,M,N分别是AB、CD的中点,两条弦的两端都在球面上运动,有下面四个命题:
①弦AB、CD可能相交于点M;
②弦AB、CD可能相交于点N;
③MN的最大值是5;
④MN的最大值是1.
其中所有正确命题的序号为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数y=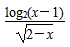
正确答案
(1,2)
解析
解析已在路上飞奔,马上就到!
知识点
10.已知x∈(-

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若n展开式的二项式系数之和为256,则n=______,其展开式中的常数项等于______.(用数字作答)
正确答案
8,70
解析
解析已在路上飞奔,马上就到!
知识点
13.等比数列{an}中,a1+a3=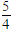
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
14.设函数f(x)=


正确答案
{-1,0}
解析
解析已在路上飞奔,马上就到!
知识点
12.已知两个向量a=(1,2),b=(x,1).若(a+2b)∥(2a-2b),则x的值为______.
正确答案
-
解析
解析已在路上飞奔,马上就到!
知识点
19.已知抛物线C:y=ax2(a>0),直线y=x+2交抛物线C于A、B两点,M是线段AB的中点,过M作x轴的垂线交抛物线C于点N.
(Ⅰ)证明:抛物线C在N点处的切线l与AB平行;
(Ⅱ)是否存在实数a,使得
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.由函数y=f(x)确定数列{an},an=f(n),函数y=f(x)的反函数y=f-1(x)能确定数列{bn},bn=f-1(n).若对于任意n∈N*都有bn=an,则称数列{bn}是数列{an}的“自反数列”.
(Ⅰ) 设函数f(x)=
(Ⅱ)已知正数数列{cn}的前n项和
(Ⅲ)在(Ⅰ)和(Ⅱ)的条件下,d1=2,当n≥2时,设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.已知△ABC的三个内角A,B,C所对的边分别为a,b,c,向量m=(1,1-
(Ⅰ)求角B;
(Ⅱ)若a+c=b,判断△ABC的形状.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.每次抛掷一枚质地均匀的骰子(六个面上分别标以数字1,2,3,4,5,6).
(Ⅰ)连续抛掷3次,求向上的点数互不相同的概率;
(Ⅱ)连续抛掷3次,求向上的点数之和为6的概率;
(Ⅲ)连续抛掷6次,求向上的点数为奇数且恰好出现4次的概率
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,已知四棱锥P-ABCD的底面是菱形,∠BCD=60°,点E是BC边的中点,AC与DE交于点O,PO⊥平面ABCD.
(Ⅰ)求证:PD⊥BC;
(Ⅱ)若AB=6,PC=6,求二面角P-AD-C的大小;
(Ⅲ)在(Ⅱ)的条件下,求异面直线PB与DE所成角的余弦值.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.设定义在R上的函数f(x)=a0x4+a1x3+a2x2+a3x+a4(a0,a1, a2,a3,a4∈R).当x=-1时f(x)取得极大值
(Ⅰ)求函数f(x)的表达式;
(Ⅱ)试在函数y=f(x)的图象上求两点,使以这两点为切点的切线互相垂直,且切点的横坐标都在区间[-

正确答案
解析
解析已在路上飞奔,马上就到!