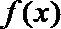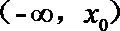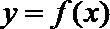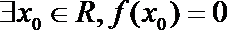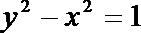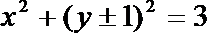- 真题试卷
- 模拟试卷
- 预测试卷
3.曲线
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.执行下面的程序框图,如果输入的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.复数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.在一个几何体的三视图中,正视图和俯视图如图所示,则相应的侧视图可以为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设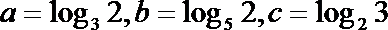
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设抛物线







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知函数y= f(x) 的周期为2,当x

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数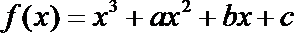
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若


正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
15.等比数列{an}的前n项和为Sn,若S3+3S2=0,则公比q=_____.
正确答案
-2
解析
解析已在路上飞奔,马上就到!
知识点
16.已知直三棱柱





正确答案
13
解析
解析已在路上飞奔,马上就到!
知识点
13.从

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设向量
(Ⅰ)若

(Ⅱ)设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,四棱锥




(I)证明:
(II)设

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸,呼吸困难等心肺疾病,为了解某市心肺疾病是否与性别有关,在某医院随机对入院50人进行了问卷调查,得到了如下的列联表.
(Ⅰ)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(Ⅱ)在上述抽取的6人中选2人,求恰有一名女性的概率;
(Ⅲ)为了研究心肺疾病是否与性别有关,请计算出统计量
下面的临界值表供参考:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.在平面直角坐标系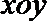
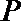
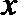
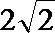
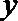
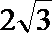
(I)求圆心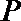
(II)若点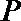
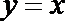
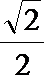
正确答案
(Ⅰ)
(Ⅱ)
解析
解析已在路上飞奔,马上就到!
知识点
21.设函数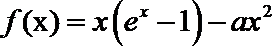
(Ⅰ)若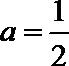
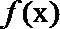
(Ⅱ)若当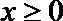
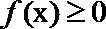
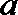
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题计分.
22.选修4-1:几何证明选讲
如图,








(Ⅰ)证明:
(Ⅱ)若


23.选修4-4:坐标系与参数方程
在直角坐标系



(Ⅰ)求C2的方程;
(Ⅱ)在以


24.选修4-5:不等式选讲
设函数

(Ⅰ)当

(Ⅱ)若不等式


正确答案
22.
23.
24.
解析
解析已在路上飞奔,马上就到!