- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合



正确答案
解析
由


考查方向
解题思路
由


易错点
本题易在审题上出问题。
知识点
5.已知等差数列



正确答案
解析
由


考查方向
解题思路
由

易错点
本题易运算上出错。
知识点
8.执行右图所示程序,则输出的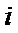
正确答案
解析
第一次运行循环体后: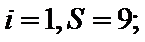

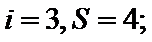
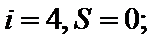
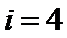
考查方向
解题思路
由程序可知,此算法在进行累减运算,以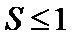
易错点
本题易在算法的中间运算中出问题。
知识点
2.设



正确答案
解析
由题设





考查方向
解题思路
分清条件与结论,显然



易错点
本题易在充分必要的判断上出问题;
知识点
3.设函数

正确答案
解析
由题设知:
考查方向
解题思路
本题考查由自变量的范围确定用对应的解析式。
易错点
本题必须注意自变量所在范围的问题,忽视则会出现错误。
知识点
4.下列函数中,最小正周期为
正确答案
解析
由最小正周期为


考查方向
解题思路
由最小正周期和关于原点对称求解出相应的解析式
易错点
本题易在对性质和三角恒等变形不到们导致出错 。
知识点
6.设


正确答案
解析
如图所示,可行域为ABCD,当经过点



考查方向
解题思路
由不等式组画出对应的可行域,再画出初始线,进而对可行域进行扫描,
易错点
作出可行域,还有就是如何衡量最大和最小,忽视则会出现错误。
知识点
7.已知双曲线


正确答案
解析
由渐近线过点




考查方向
解题思路
1、由渐近线所过的点求出



易错点
本题易在等量关系计算上出问题。
知识点
9.设复数


正确答案
解析
考查方向
解题思路
由复数的几何意义得出事件的测度——面积。
易错点
对复数的几何意义不清和概型错误。
知识点
10.已知



正确答案
解析
由函数





考查方向
解题思路
1、由选项找到解题方向——即

易错点
找不到解题的切入点。
知识点
11.某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率(材料利用率=新工件体积/原工件体积)为( )
正确答案
解析
由题设知:








考查方向
解题思路
由三视图先还原出实物的直观图,再计算出内接长方体的最大体积。
易错点
1、无法由三视图还原出实物直观图。2、圆锥内接长方体不会处理。
知识点
12.将正奇数排成如图所示的三角形数阵(第







正确答案
解析
由







考查方向
解题思路
由数的排列特点找到对应的规律。
易错点
本题易规律的寻找上出错。
知识点
14、若曲线



正确答案
考查方向
解题思路
本题考查导数的几何意义——切线问题,解题步骤如下:
易错点
是在运算上出错。
知识点
15.已知定点





正确答案
9
考查方向
解题思路
本题主要考查了双曲线的定义和数形结合思想,解题步骤如下:
易错点
本题难在定义的应用和几何关系的寻找。
知识点
13.袋中有形状、大小都相同的4个球,其中1个白球,1个红球,2个黄球。从中一次随机取出2个球,则这2个球颜色不同的概率为 .
正确答案
考查方向
解题思路
本题考查古典概型,解题步骤如下:
易错点
审题不清和考虑不全面导致出错。
知识点
16.定义在






正确答案
考查方向
易错点
1、函数

知识点
如图,在四棱锥









22.求证:平面

23.求点

正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,根据题设先证线面垂直再去证面面垂直;证明:取






















考查方向
解题思路
本题考查了面面垂直的证明和点到面的距离的求,解题步骤如下:根据题设先证线面垂直再去证面面垂直。
易错点
对面面垂直的证明的表述不严谨和运算出错
正确答案
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难,由等体积法求出点到面的距离。由⑴知,
∴








∴点


考查方向
解题思路
本题考查了面面垂直的证明和点到面的距离的求,解题步骤如下:由等体积法求出点到面的距离。
易错点
对面面垂直的证明的表述不严谨和运算出错
已知



17.若

18.若


正确答案
解析
试题分析:本题属于三角恒等变形和解三角形的基本问题,对

又


考查方向
解题思路
本题考查解三角形,解题步骤如下:对

易错点
对

正确答案

解析
试题分析:本题属于三角恒等变形和解三角形的基本问题,由方程思想求解出边长再算出面积;由17可知






考查方向
解题思路
本题考查解三角形,解题步骤如下:由方程思想求解出边长再算出面积。
易错点
根据条件合理选择定理来解三角形。
已知椭圆

24.求椭圆
25.设直线









正确答案

解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,由方程思想求解出标准方程; 由已知设椭圆


由



考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和最值问题——函数思想,解题步骤如下:由方程思想求解出标准方程;
易错点
无法构建关于点

正确答案
解析
试题分析:本题属于圆锥曲线的基本问题,题目的难度是逐渐由易到难,(构建关于点




则由



设点

∵四边形





从而

又点


当且仅当
当直线


从而点







∴点


考查方向
解题思路
本题考查圆锥曲线中求标准方程的方法和最值问题——函数思想,解题步骤如下:构建关于点

易错点
运算和斜率不存在的讨论。
某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为
19.求频率分布图中
20.估计该企业的职工对该部门评分不低于80的概率;
21.从评分在

正确答案

解析
试题分析:本题属于统计与概率的常见题型,题目的难度是比较稳定,属于中档偏易题,由频率之和为1求解出


考查方向
解题思路
本题主要考查了统计、古典概型,解题步骤如下:由频率之和为1求解出
易错点
审题不清和考虑不全面导致出错。
正确答案

解析
试题分析:本题属于统计与概率的常见题型,题目的难度是比较稳定,属于中档偏易题,由频率估计出相应概率;
由所给频率分布直方图知,50名受访职工评分不低于80的频率为
∴该企业职工对该部门评分不低于80的概率估计值为
考查方向
解题思路
本题主要考查了统计、古典概型,解题步骤如下:由频率估计出相应概率。
易错点
审题不清和考虑不全面导致出错。
正确答案

解析
试题分析:本题属于统计与概率的常见题型,题目的难度是比较稳定,属于中档偏易题,用列举法求出所有基本事件数和符合所求事件数,再算出对应概率。
受访职工评分在


受访职工评分在






考查方向
解题思路
本题主要考查了统计、古典概型,解题步骤如下:用列举法求出所有基本事件数和符合所求事件数,再算出对应概率。
易错点
审题不清和考虑不全面导致出错。
设函数





26.求


27.设


正确答案

解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,由函数的奇偶性形成方程组求解出



联立①②解得





考查方向
解题思路
本题考查导数的应用,解题步骤如下:函数的奇偶性形成方程组求解出
易错点
对求解析式方法不熟导致出错。
正确答案
详见解析;
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,由函数的奇偶性形成方程组求解出



联立①②解得





考查方向
解题思路
本题考查导数的应用,解题步骤如下:
观察所证不等式的结构构建新函数去证明所求不等式。
易错点
未发现
选修4-1:几何证明选讲
如图,






28.求证:
29.求证:
正确答案
详见解题过程;
解析
试题分析:本题属于平面几何的基本问题,由圆的性质直接导出角关系。∵




考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。
正确答案
详见解题过程
解析
试题分析:本题属于平面几何的基本问题,由相似关系去证所证。连接





考查方向
解题思路

易错点
对图形的分析不到位和定理不熟练导致出错。