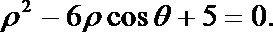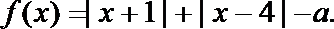- 真题试卷
- 模拟试卷
- 预测试卷
2.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
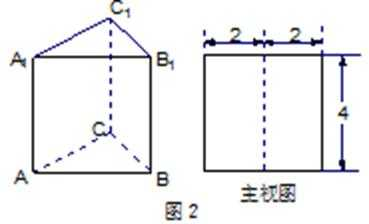
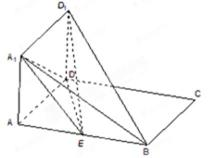
3.如图2,正三棱柱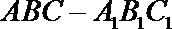
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若
①存在一条直线

②存在一个平面

③存在两条平行直线


④存在两条异面直线


那么可以是

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若直线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图,在等腰直角









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下面程序执行后输出的结果是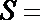
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若三棱锥







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.有下列命题:
①函数

②函数

③关于


④已知命题


⑤线性回归方程



其中所有真命题的序号是___________.
正确答案
③④
解析
解析已在路上飞奔,马上就到!
知识点
13.已知数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.设椭圆的焦点为



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.设


(1)求
(2)设





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.某校高三(1)班全体女生的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:
(1)求高三(1)班全体女生的人数;
(2)求分数在

(3)若要从分数在

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知曲线








(1)求曲线
(2)直线








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图所示,正方形
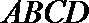
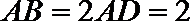
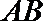
(1)求证: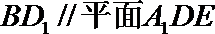
(2)求证: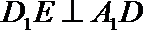
(3)求点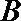
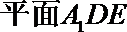
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.设关于






(1)求实数
(2)若函数


(3)设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题计分.
22.选修4—1:几何证明选讲
如图,已知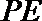
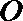
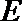

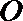

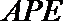
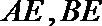
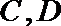
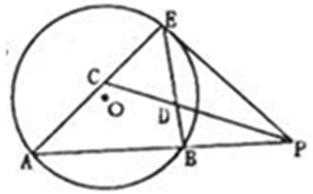
求证:
(1)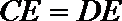
(2)
23.选修4—4:坐标系与参数方程
在直角坐标系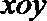
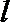
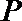
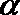
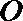
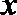
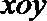
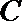
(1)若直线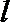
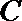
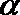
(2)设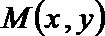
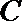
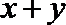
24.选修4—5:不等式选讲
设函数
(1)当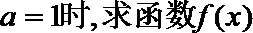
(2)若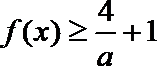
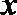
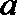
正确答案
22.

23.
24.
解析
解析已在路上飞奔,马上就到!