- 真题试卷
- 模拟试卷
- 预测试卷
4.设平面区域D是由双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.“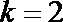
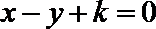
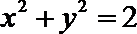
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.从正四面体的6条棱中随机选择2条,则这2条棱所在直线互相垂直的概率为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.全集

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知下列命题:
①命题



②回归直线一定过样本中心(
③若

其中正确命题的个数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知点





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如果函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知某几何体的三视图如图所示,则该几何体的表面积为_____________。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.下面的程序框图输出的结果为_____________。
正确答案
-3
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如果对于任意一个三角形,只要它的三边长



①
②
③
④
⑤
则其中是 “保三角形函数”的有_____________。(写出所有正确的序号)
正确答案
①④
解析
解析已在路上飞奔,马上就到!
知识点
14.已知在





正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
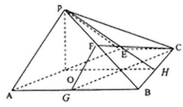
19.如图,在矩形
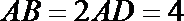
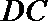
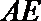
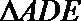
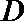
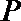

(Ⅰ)若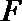

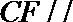
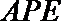
(Ⅱ)求证:面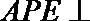
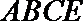
(Ⅲ)求三棱锥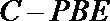
正确答案
(Ⅰ)
取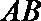
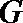
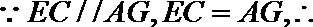
在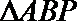
又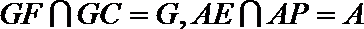
所以平面APE//平面FGC
又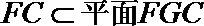
(Ⅱ)取AE中点O,连接PO,则
取BC的中点H,连OH,PH,
因为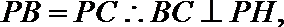
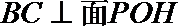
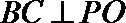
又BC与AE相交,可得
所以,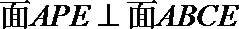
(Ⅲ)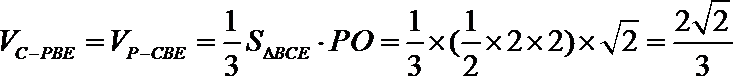
解析
解析已在路上飞奔,马上就到!
知识点
18.设函数


(Ⅰ)求数列
(Ⅱ)当



正确答案
解:(Ⅰ)



所以
(Ⅱ)当

则
两式相减得

所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(Ⅰ)当

(Ⅱ)若


正确答案
解:(Ⅰ)函数
当
当




极小值是
(Ⅱ)由
又函数

则



即

设


所以


解析
解析已在路上飞奔,马上就到!
知识点
16.已知向量


(Ⅰ)求函数
(Ⅱ)在



正确答案
解:(Ⅰ)

(Ⅱ)由

又


解析
解析已在路上飞奔,马上就到!
知识点
17.某校高三数学竞赛初赛考试后,对考生的成绩进行统计(考生成绩均不低于90分,满分为150分),将成绩按如下方式分成六组,第一组


(Ⅰ)求第四和第五组频率,并补全频率分布直方图;
(Ⅱ)若不低于120分的同学进入决赛,不低于140分的同学为种子选手,完成下面
正确答案
解:(Ⅰ)设第四,五组的频率分别为


由①②解得
从而得出直方图(如图所示)
(Ⅱ)依题意,进入决赛人数为
进而填写列联表如下:
又由
故没有99﹪的把握认为“进入决赛的同学成为种子选手与专家培训有关”.
解析
解析已在路上飞奔,马上就到!
知识点
21.已知椭圆


(Ⅰ)求椭圆
(Ⅱ)若过点






正确答案
解:(Ⅰ)由题知


又因为


故椭圆

(Ⅱ)由题意知直线
设




由




∵



∵点

∴

∴
解析
解析已在路上飞奔,马上就到!