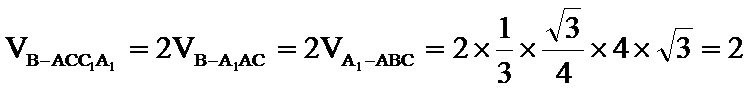- 真题试卷
- 模拟试卷
- 预测试卷
1. 定义在R上的奇函数f(x)以2为周期,则f(1) =_________
正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
2.如果复数

正确答案
0
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
(2a,-a)
解析
解析已在路上飞奔,马上就到!
知识点
6.数列{an}满足:an=

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.老师告诉学生小明说,“若O为△ABC所在平面上的任意一点,且有等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.若函数y=ax(a>1)和它的反函数的图像与函数y=

正确答案
8.4
解析
解析已在路上飞奔,马上就到!
知识点
3.若

正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
7.某市为加强城市圈的建设,计划对周边如图所示的A、B、C、D、E、F、G、H八个中小城市进行综合规划治理,第一期工程拟从这八个中小城市中选取三个城市,但要求没有任何两个城市相邻,则城市A被选中的概率为________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.点P是椭圆

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.在△ABC中,已知|AB|=2,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.如图为一几何体的的展开图,其中ABCD是边长为6的正方形,SD=PD=6,CR=SC,AQ=AP,点S,D,A,Q及P,D,C,R共线,沿图中虚线将它们折叠,使P,Q,R,S四点重合,则需要________个这样的几何体,就可以拼成一个棱长为12的正方体.
正确答案
24
解析
解析已在路上飞奔,马上就到!
知识点
16.数列{an}满足:a1=


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.在


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若点M(a,



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若函数y=cos2x与y=sin(x+φ)在[0,
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数

(1)求f(x)的解析式;
(2)作出f(x)在[0,π]范围内的大致图象.
正确答案
(1)f(x)=1–sin
(2)略
解析
解析已在路上飞奔,马上就到!
知识点
18.设虚数z满足|2z+15|=

(1)计算|z|的值;
(2)是否存在实数a,使
正确答案
(1)|z|=5
(2)a=±5
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,已知斜三棱柱ABC-A1B1C1的各棱长均为2,侧棱与底面所成角为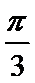
(1)判断B1C与C1A是否垂直,并证明你的结论;
(2)求四棱锥B-ACC1A1的体积。
正确答案
(1)几种常见处理方法:用空间直角坐标系解、传统方法解、基向量解.
(2)
解析
解析已在路上飞奔,马上就到!
知识点
20.在新的劳动合同法出台后,某公司实行了年薪制工资结构改革。该公司从2008年起,每人的工资由三个项目构成,并按下表规定实施:
如果该公司今年有5位职工,计划从明年起每年新招5名职工。
(1)若今年(2008年)算第一年,将第n年该公司付给职工工资总额y(万元)表示成年限n的函数;
(2)若公司每年发给职工工资总额中,房屋补贴和医疗费的总和总不会超过基础工资总额的p%,求p的最小值。
正确答案
(1)y=10n(1+10%)n+0.2n2+1.8n , n
(2)由0.2n2+1.8n≤10n-1.1n-p%,得p%≥
令an=
由
∴p%≥a1=a2=
∴p≥
解析
解析已在路上飞奔,马上就到!
知识点
22.若给定椭圆C:ax2+by2=1(a>0,b>0,a
(1)若N(x0,y0)在椭圆C上,判断椭圆C与它的“伴随直线”的位置关系(当直线与椭圆的交点个数为0个、1个、2个时,分别称直线与椭圆相离、相切、相交),并说明理由;
(2)命题:“若点N(x0,y0)在椭圆C的外部,则直线l与椭圆C必相交.”写出这个命题的逆命题,判断此逆命题的真假,说明理由;
(3)若N(x0,y0)在椭圆C的内部,过N点任意作一条直线,交椭圆C于A、B,交l于M点(异于A、B),设


正确答案
(1)
即ax2–2ax0x+ax02=0
∴△=4a2x02–4a2x02=0
∴l与椭圆C相切.
(2)逆命题:若直线l:ax0x+by0y=1与椭圆C相交,则点N(x0,y0)在椭圆C的外部,是真命题。
联立方程得(aby02+a2x02)x2–2ax0x+1–by02=0
则△=4a2x02–4a(by02+ax02)(1–by02)>0
∴ax02–by02+b2y04–ax02+abx02y02>0
∴by02+ax02>1
∴N(x0,y0)在椭圆C的外部.
(3)同理可得此时l与椭圆相离,
设M(x1,y1),A(x,y)
则
代入椭圆C:ax2+by2=1,
利用M在l上,
即ax0x1+by0y1=1,
整理得(ax02+by02–1)
同理得关于
即


∴

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=(|x|-b)2+c,函数g(x)=x+m,
(1)当b=2,m=-4时,f(x)
(2)当c=-3,m=-2时,方程f(x)=g(x)有四个不同的解,求实数b的取值范围。
正确答案
(1)c≥x–4–(|x|–2)2=

(2)(|x|–b)2–3=x–2,即(|x|–b)2=x+1有四个不同的解,
∴ (x–b)2=x+1(x≥0)有两个不同解以及(x+b)2=x+1(x<0)也有两个不同解,
由根的分布得b≥1且1<b<
∴1<b<
解析
解析已在路上飞奔,马上就到!