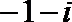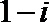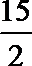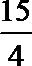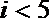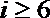- 真题试卷
- 模拟试卷
- 预测试卷
5.某一个班全体学生参加历史测试,成绩的频率分布直方图如图,则该班的平均分估计是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数













正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.复数
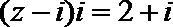

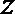
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.命题“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设公比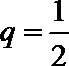

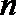

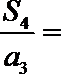
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.将函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.一个几何体的三视图如图所示,则这个几何体的体积为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知全集


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
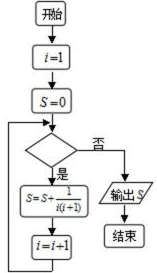
7.一个算法的程序框图如图所示,若该程序输出的结果为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.抛物线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.一艘船以均匀的速度由A点向正北方向航行,如图,开始航行时,从A点观测灯塔C的方位角(从正北方向顺时针转到目标方向的水平角)为45°,行驶60海里后,船在B点观测灯塔C的方位角为75°,则A到C的距离是________海里.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
选做题(14、15题,只能从中选做一题)
14. (坐标系与参数方程选做题)
曲线







15.(几何证明选讲选做题)
如图,








正确答案
14.
15.
解析
解析已在路上飞奔,马上就到!
知识点
17.某校为了解高三年级不同性别的学生对体育课改上自习课的态度(肯定还是否定),进行了如下的调查研究.全年级共有


(1)求抽取的男学生人数和女学生人数;
(2)通过对被抽取的学生的问卷调查,得到如下
①完成列联表;
②能否有
(3)若一班有





现从这
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数f(x)=x2-2(n+1)x+n2+5n-7.
(1)设函数y=f(x)的图象的顶点的纵坐标构成数列{an},求证:{an}为等差数列;
(2)设函数y=f(x)的图象的顶点到x轴的距离构成数列{bn},求{bn}的前n项和Sn.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数
(1)求
(2)若函数

(3)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求函数f(x)的表达式;
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 如图,已知抛物线










(1)求抛物线
(2)当


(3)若直线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知四棱柱



(Ⅰ)求证:
(Ⅱ)求点

正确答案
解析
解析已在路上飞奔,马上就到!