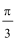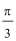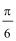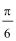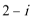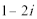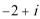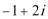文科数学 2013年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

9.要得到函数的图象，只需将函数的图象（）

A左移个单位

B右移个单位

C右移个单位

D左移个单位

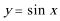
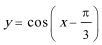
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明

题型：单选题

分值: 5分

10．已知当椭圆的长轴、短轴、焦距依次成等比时称椭圆为“黄金椭圆”，请用类比的性质定义“黄金双曲线”，并求“黄金双曲线”的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：单选题

分值: 5分

12．对于函数，若存在区间，使得，则称区间为函数的一个“稳定区间”．现有四个函数：

①

②

③

④

其中存在“稳定区间”的函数有（）

A①②

B②③

C③④

D②④

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

分值: 5分

8.已知直线丄平面，直线平面，则“”是“”的（）

A充要条件

B必要条件

C充分条件

D既不充分又不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

4．在中，若,，，则的面积为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

同角三角函数间的基本关系正弦定理

题型：单选题

分值: 5分

6．等比数列的各项均为正数，且，则（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：单选题

分值: 5分

3．若直线与直线垂直，则的值是（　　）

A或

B或

C或

D或1

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

两条直线垂直与倾斜角、斜率的关系

题型：单选题

分值: 5分

5．下列函数中,既是偶函数,又在区间内是增函数的为（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的判断与证明函数奇偶性的判断

题型：单选题

分值: 5分

11.将直线绕着其与轴的交点逆时针旋转得到直线m，则m与圆截得弦长为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

7．设抛物线上一点P到y轴的距离是4，则点P到该抛物线的焦点的距离是（）

D12

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的标准方程和几何性质

题型：单选题

分值: 5分

2．已知A＝｛｝，B＝｛｝，则A∪B＝（）

A[0, 1]

B（2, ＋∞）

C[0, 2]

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

并集及其运算

题型：单选题

分值: 5分

1．复数=（）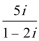

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复数代数形式的乘除运算

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

13. 如图所示一个空间几何体的三视图（单位）则该几何体的体积为 _______

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：填空题

分值: 4分

16．如图都是由边长为1的正方体叠成的几何体,例如第（1）个几何体的表面积为6个平方单位，第（2）个几何体的表面积为18个平方单位，第（3）个几何体的表面积是36个平方单位.依此规律,则第个几何体的表面积是__________个平方单位。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数单调性的性质

题型：填空题

分值: 4分

15．点是不等式组表示的平面区域内一动点，定点是坐标原点，则的取值范围是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

14．已知m>0,n>0,向量，且，则的最小值是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

一元高次不等式的解法

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19. 已知函数。

（Ⅰ）求函数的最小值和最小正周期；

（Ⅱ）已知内角的对边分别为，且，若向量与共线，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：简答题

分值: 12分

20．椭圆：的左、右焦点分别为，焦距为2，，过作垂直于椭圆长轴的弦长为3．

（Ⅰ）求椭圆的方程；

（Ⅱ）若过的直线l交椭圆于两点．并判断是否存在直线l使得的夹角为钝角，若存在，求出l的斜率k的取值范围。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：简答题

分值: 12分

17. 在数列中，为常数，，且成公比不等于1的等比数列。

（Ⅰ）求的值；

（Ⅱ）设，求数列的前项和

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：简答题

分值: 12分

21．某企业投入81万元经销某产品，经销时间共60个月，市场调研表明，该企业在经销这个产品期间第个月的利润（单位：万元），为了获得更多的利润，企业将每月获得的利润投入到次月的经营中，记第个月的当月利润率，例如：．

（Ⅰ）求；

（Ⅱ）求第个月的当月利润率；

（Ⅲ）该企业经销此产品期间，哪个月的当月利润率最大，并求该月的当月利润率。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

求线性目标函数的最值

题型：简答题

分值: 12分

18.在几何体ABCDE中，∠BAC=，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1

（Ⅰ）求证：DC∥平面ABE；

（Ⅱ）求证：AF⊥平面BCDE；

（Ⅲ）求证：平面AFD⊥平面AFE。

18．在几何体ABCDE中，∠BAC=，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1

（Ⅰ）求证：DC∥平面ABE；

（Ⅱ）求证：AF⊥平面BCDE；

（Ⅲ）求证：平面AFD⊥平面AFE．

第(1)小题正确答案及相关解析

正确答案

题型：简答题

分值: 14分

22.已知函数处取得极值2.

（Ⅰ）求函数的表达式；

（Ⅱ）当满足什么条件时，函数在区间上单调递增？

（Ⅲ）若为图象上任意一点，直线与的图象切于点P，求直线的斜率的取值范围。

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

正确答案

解析

知识点

文科数学热门试卷