- 真题试卷
- 模拟试卷
- 预测试卷
4. 函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6. 已知正整数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设等比数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 如果
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 等差数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 不等式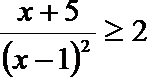
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3. 已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 幂函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 向50名学生调查对A、B两事件的态度,有如下结果:赞成A的人数是全体的五分之三,其余的不赞成,赞成B的比赞成A的多3人,其余的不赞成;另外,对A、B都不赞成的学生数比对A、B都赞成的学生数的三分之一多1人,对A、B都不赞成的学生有__________。
正确答案
8
解析
解析已在路上飞奔,马上就到!
知识点
14. 给出定义:若





①函数

②函数

③函数
④函数

其中正确的命题的序号是__________。
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
10. 若函数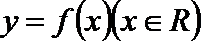
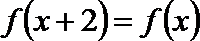
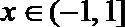
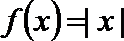
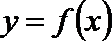
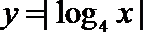
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 






正确答案


∴
由已知:
∴
解析
解析已在路上飞奔,马上就到!
知识点
16. 已知二次函数


(1)若方程

(2)若

正确答案
(1)∵
∴

因而
由方程

因为方程②有两个相等的根,所以
即


由于
将

(2)由
又

由

故当

解析
解析已在路上飞奔,马上就到!
知识点
18. 数列





(1)求
(2)
(3)求证:
正确答案
(1)因为


所以

所以
由
所以:


(2)∵
∴
∴
∴
∴




(3)
解析
解析已在路上飞奔,马上就到!
知识点
19. 设函数


(I)若直线




(II)若函数

正确答案
(I)由


由


i)当
ii)当



(II)
i)若函数








ii)若函数








综上可得,若函数


解析
解析已在路上飞奔,马上就到!
知识点
17. 已知



(I)当


(II)求函数

(III)若在区间



正确答案
由

(I)当

所以

(II)令
(1) 当

故


(2)当


所以

(III)设
对

因为





依题意,只需

即

所以正实数

解析
解析已在路上飞奔,马上就到!
知识点
20. 数列



(1)设


(2)设





正确答案
(I)由已知可得

即
∴
累加得
又
(II)由(I)知
∴
易知
∴
∴

解析
解析已在路上飞奔,马上就到!