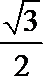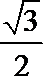- 真题试卷
- 模拟试卷
- 预测试卷
2.设z=1+i(i是虚数单位),则
正确答案
解析

考查方向
本题主要考查复数的运算
解题思路
直接计算
易错点
本题易在求共轭复数时发生错误。
知识点
4.函数f(x)=x cosx在点(0,f(0))处的切线斜率是
正确答案
解析
f’(x)=cosx-xsinx,得k=f’(0)=1。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查导数的几何意义
解题思路
直接求导,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在求导数时发生错误。
知识点
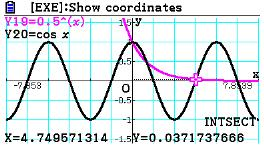
5.已知函数f(x)=
正确答案
解析
由图可知,2个函数图像有3个交点。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查函数图像及零点
解题思路
1、分别画出2个函数图像;
2、求出交点个数,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在画图时发生错误。
知识点
6.按如下程序框图,若输出结果为273,
则判断框内?处应补充的条件为
正确答案
解析
由题可知,S=0+31+33+35=273,得i=7。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
本题主要考查流程图
解题思路
按照流程图所示依次代入计算,即可得到结果。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在判断循环次数时发生错误。
知识点
7.设双曲线

正确答案
解析
由c=1,且焦点在y轴上,得a=2b。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
本题主要考查双曲线的标准方程
解题思路
1、求出c;
2、利用a,b,c关系求a,b,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在判断焦点位置时发生错误。
知识点
9.右图是一个四面体的三视图,这三个视图均是腰长为2的等腰直角三角形,正视图和俯视图中的虚线是三角形的中线,则该四面体的体积为
正确答案
解析
由图可知,此几何体为底边长分别为1,2,高为2的三棱锥。B选项不正确,C选项不正确,D选项不正确,所以选A选项。本题主要考查三视图
考查方向
本题主要考查三视图
解题思路
1、还原几何体;
2、求出体积,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在还原几何体时发生错误。
知识点
1.设全集U={x∈N﹡|x≤4},集合A={1,4},B={2,4},则
正确答案
解析
A∩B={4}, 
考查方向
本题主要考查集合的交集、补集运算
解题思路
1、求出A∩B;
2、求出
易错点
本题易在求补集时发生错误。
知识点
3.cos160°sin10°-sin20°cos10°=
正确答案
解析
cos160°sin10°-sin20°cos10°=-cos20°sin10°-sin20°cos10°=-sin30O=-
考查方向
本题主要考查两角和差公式
解题思路
直接计算,即可得到结果。A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在转化角度时发生错误。
知识点
8.正项等比数列{

正确答案
解析

考查方向
本题主要考查极值和数列、对数运算
解题思路
1、求出a1,a4031;2、求出a2016,即可得到结果。A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在求a2016时发生错误。
知识点
10.已知函数f(x)=x+




正确答案
解析
f(x)min=f(1)=5, g(x)min = g(2)=4+a,得a≤1。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
本题主要考查函数的值域
解题思路
1、求出f(x)在[
2、求出f(x)min≥g(x)min,即可得到结果。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断范围大小时发生错误。
知识点
11.已知椭圆
正确答案
解析
设F1A=x, F2A=y,由题可知,x+y=2a,x2+y2=4c2,2x+√2x=4a,联立方程组,代换得a2(9-6√2)=c2,即e=

考查方向
本题主要考查直线与椭圆的位置关系
解题思路
1、用a,c表示出F1A,F2A;
2、将所求式子联立,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在表示a, c关系时发生错误。
知识点
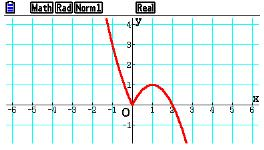
12.已知函数f(x)=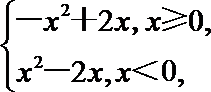
正确答案
解析
设f(x)=t,方程 t2+at-b2=0的两根分别为t1、t2,则t1t2=-b2≤0.若b≠0,则t1、t2异号,由函数图像可知,对应的x值不唯一,因此,b=0。即不等式的解为-a<t<0.注意到t=0时x=0,或x=2.因此a的最大值为8。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
本题主要考查分段函数和不等式
解题思路
1、画出f(x)的图像;
2、利用方程只有一个整数解求解,即可得到结果。A选项不正确,B选项不正确,C选项不正确,所以选D选项。
易错点
本题易在处理只有一个整数解时发生错误。
知识点
14.若不等式

正确答案
解析
由题可知SM=2π,SN=48,则P=
考查方向
本题主要考查线性规划及几何概型。
解题思路
解题步骤如下:1、画出平面区域。2、利用概率公式求解.
易错点
本题必须注意利用图像完成。
知识点
16.已知向量α,β是平面内两个互相垂直的单位向量,若(5α-2γ)·(12β-2γ)=0,则|γ|的最大值是____________.
正确答案
解析
由题可知,(5α-2γ)·(12β-2γ)=4γ2-2γ(α+12β)=0,则γ2≤(
考查方向
本题主要考查了平面向量的垂直关系。
解题思路
解题步骤如下:利用公式求解。
易错点
本题要注意单位向量。
知识点
17.已知等差数列{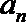
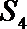
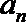
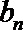
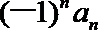
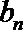
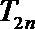
正确答案
an=4n-3; T2n=4n
解析
⑴由已知条件: 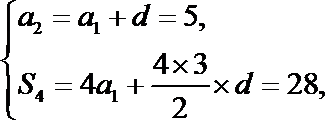
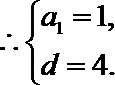
⑵由⑴可得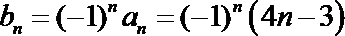
考查方向
本题主要考查数列的综合运算
易错点
本题易在求和时发生错误。
知识点
19.如图,矩形CDEF和梯形ABCD互相垂直,∠BAD=∠ADC=90°,AB=AD=
正确答案
(1)略;(2)
解析
⑴证明:设






因为

所以

又因为



所以

⑵解:取









所以

同理

所以,



所以四边形

所以

又因为

所以
又

所以


注意到


所以
考查方向
本题考查了立体几何中的线面平行和体积.属于考中的高频考点。
解题思路
本题考查立体几何,解题步骤如下:
1、转化为证明线线平行。
2、利用体积公式求解。
易错点
第一问中的线面平行的转化。
知识点
13.函数f(x)=
正确答案
解析
由题可知,2x-1≥0,即x≥0.本题主要考查了函数的定义域。
考查方向
本题主要考查了函数的定义域。
解题思路
解题步骤如下:利用不等式求解。
易错点
本题要注意解指数不等式。
知识点
15.△ABC的三个内角为A、B、C,若

正确答案
1
解析
由题可知,A=45o,可求得tanA=1.本题主要考查了三角函数的公式化简。
考查方向
本题主要考查了三角函数的公式化简。
解题思路
解题步骤如下:利用两角和差公式求解。
易错点
本题要注意公式的化简。
知识点
18.为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
(Ⅰ)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民分为两类:A类市民在罚金不超过10元时就会改正行为;B类是其他市民.现对A类与B类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为B类市民的概率是多少?
正确答案
(1)会降低

解析
⑴设“当罚金定为10元时,闯红灯的市民改正行为”为事件

∴当罚金定为10元时,比不制定处罚,行人闯红灯的概率会降低
⑵由题可知































∴抽取4人中前两位均为

考查方向
本题考查了概率统计问题.属于高考中的高频考点
解题思路
1、求出相应的概率
2、利用列举法求解。
易错点
概率表示。
知识点
20.已知点M(-1,0),N(1,0),曲线E上任意一点到点M的距离均是到点N距离的
(Ⅰ)求曲线E的方程;
(Ⅱ)已知m≠0,设直线l1:x-my-1=0交曲线E于A,C两点,直线l2:mx+y-m=0交曲线E于B,D两点.若CD的斜率为-1,求直线CD的方程.
正确答案
(1)
(2)y=-x,或y=-x+3.
解析
(1)直接按照步骤来求
(2)要注意对参数的讨论.
⑴解:设曲线

由题意,
整理得

⑵解:由题知

设曲线


线段



设直线

由

由圆的几何性质,





所以直线


考查方向
本题考查了圆的标准方程和直线与圆的位置关系,属于高考中的高频考点.
解题思路
解题步骤如下:
1、利用已知求解。
2、联立直线与圆方程求解。
易错点
第二问中表示直线斜率时容易出错。
知识点
21.设函数f(x)=

(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)当m≥1时,讨论函数f(x)与g(x)图象的交点个数.
正确答案
(1)当






解析
(1)直接按照步骤来求;
(2)要注意对参数的讨论.
⑴解:函数


当



当




当


综上:当






⑵解:令

当

当

当





当












当













综上,函数
考查方向
本题考查了利用导数求含参数的函数极值,分类讨论,讨论点大体可以分成以下几类:
1、根据判别式讨论;
2、根据二次函数的根的大小;
3、定义域由限制时,根据定义域的隐含条件;
4、求导形式复杂时取部分特别常常只需要转化为一个二次函数来讨论;
5、多次求导求解等.
解题思路
1、求导,然后解导数不等式,求单调区间。
2、对参数分类讨论得结论。
易错点
第二问中的易丢对a的分类讨论。
知识点
本题为选做题,请考生在第22、23、24三题中任选一题做答。如果多做。则按所做的第一题记分.作答时用2B铅笔在答题卡上把所选题目的题号涂黑.。
22.选修4—l:几何证明选讲如图,∠BAC的平分线与BC和△ABC的外接圆分别相交于D和E,延长AC交过D、E、C三点的圆于点F.(Ⅰ)求证:EC=EF;(Ⅱ)若ED=2,EF=3,求AC·AF的值.
23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C1的参数方程为


(Ⅰ)求曲线C2的直角坐标方程;(Ⅱ)求曲线C2上的动点M到曲线C1的距离的最大值.
24.(本小题满分10分)选修4—5:不等式选讲 已知函数f(x)=|x-2|-|x+1|.
(Ⅰ)解不等式f(x)>1;(Ⅱ)当x>0时,函数g(x)=
正确答案
22.略.23.(1)



解析
22.试题分析:本题属于平面几何中的基本问题,题目的难度是容易题。
⑴证明:
因为



所以
所以
⑵解:因为

所以

由⑴知,
所以
所以
23.试题分析:本题属于参数方程中的基本问题,题目的难度是容易题。
⑴解:

可得
故

⑵解:

由⑴知曲线



所以动点


24.试题分析:本题属于不等式中的基本问题,题目的难度是容易题。
⑴解:当

当


当


综上,原不等式的解集是
⑵解:因为

所以

所以


考查方向
22.本题考查了平面几何的知识,主要涉及直线与圆的位置关系,三角形相似的考查.
23.本题考查了参数方程的知识,主要涉及直线与圆的位置关系.
24.本题考查了不等式的知识,主要涉及绝对值不等式的解法.
解题思路
22. 1、利用圆的相关定理证明。2、利用切割线定理和相交弦定理证明。
23.本题考查参数方程的知识,解题步骤如下:1、利用公式消参。2、可以利用普通方程求解。
24.本题考查不等式的知识,解题步骤如下:1、利用公式解绝对值不等式。2、可以利用图像求解。
易错点
22.相关的定理容易混用。
23.消参的过程容易出错。
24.去绝对值时容易出错。