- 真题试卷
- 模拟试卷
- 预测试卷
3.等差数列


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知等比数列





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知

正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
15.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.我们把形如



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在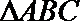
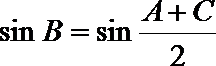
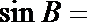
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知等比数列
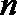
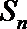
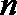
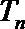


正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
13.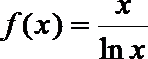
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知向量




(1)求
(2) 求函数

正确答案
(1)由题意
由题意,函数周



(2)由(1)知
又x


解析
解析已在路上飞奔,马上就到!
知识点
20.数列



(1)求数列
(2)正项等差数列





正确答案
(1)由

两式相减得
又
故



∴
(2)设



故可设
又
解得

∴

∴
解析
解析已在路上飞奔,马上就到!
知识点
21.设二次函数
①当



②当

(1)求
(2)求
(3)求最大的实数



正确答案
(1)在②中令x=1,有1≤f(1)≤1,故f(1)=1
(2)由①知二次函数的关于直线x=-1对称,
且开口向上故设此二次函数为f(x)=a(x+1)2,(a>0),
∵f(1)=1,∴a=

(3)假设存在t∈R,只需x∈[1,m],就有f(x+t)≤x.f(x+t)≤x

令g(x)=x2+(2t-2)x+t2+2t+1,g(x)≤0,x∈[1,m].
∴m≤1-t+2

∴m的最大值为9.
解析
解析已在路上飞奔,马上就到!
知识点
22.已知




(I)用


(II)求证:当

正确答案
令

当


当

故


于是

(Ⅱ)设
解析
解析已在路上飞奔,马上就到!
知识点
19.在



(I)若

(II)若

正确答案
(I)由
即
解得:
而
解析
解析已在路上飞奔,马上就到!