文科数学 2012年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

2．集合，集合，若集合，则实数的取值范围是（　　）

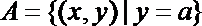
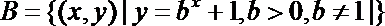
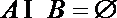
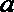
正确答案

解析

解析已在路上飞奔，马上就到！

知识点

解三角形的实际应用

题型：单选题

分值: 5分

1. 已知i为虚数单位，为实数，复数在复平面内对应的点为M，则“”是“点M在第四象限”的（　　）

A充分而不必要条件

B必要而不充分条件

C充要条件

D既不充分也不必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的单调性与特殊点

题型：单选题

分值: 5分

7. 设e<x<10，记a=ln(lnx)，b=lg(lgx)，c=ln(lgx)，d=lg(lnx)，则a，b，c，d的大小关系（　　）

Aa<b<c<d

Bc<d<a<b

Cc<b<d<a

Db<d<c<a

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

分值: 5分

8.已知函数的定义域为，当时，，且对任意的实数x、y，等式恒成立，若数列满足，且，则的值为（　　）

A4019

B4020

C4021

D4023

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：单选题

分值: 5分

6.已知是自然对数底数，若函数的定义域为，则实数的取值范围为（　　）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：单选题

分值: 5分

9.在算式“”中，都为正整数，且它们的倒数之和最小，则的值分别为（　　）

A10，5

B6，6

C14，4

D18，3

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

相等向量与相反向量

题型：单选题

分值: 5分

4. 要测量顶部不能到达的电视塔AB的高度, 在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°, CD=40m, 则电视塔的高度为（　　）

A10m

B20m

C20m

D40m

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：单选题

分值: 5分

5．将函数的图象向左平移个单位，若所得的图象与原图象重合，则的值不可能等于（　　）

D12

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求参数的取值范围

题型：单选题

分值: 5分

10.如图，在等腰梯形ABCD中，AB∥CD,且AB=2AD，设,以A,B为焦点且过点D的双曲线离心率为，以C,D为焦点且过点A的椭圆的离心率为，则（　　）

A随着角的增大，增大，为定值

B随着角的增大，减小，为定值

C随着角的增大，增大，也增大

D随着角的增大，减小，也减小

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

3．某市质量监督局计量认证审查流程图如图示：

从上图可得在审查过程中可能不被通过审查的环节有（　　）

A 1处

B 2处

C 3处

D 4处

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

填空题本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。

题型：填空题

分值: 5分

11．一个总体分为A、B两层，其个体数之比为4﹕1 ，用分层抽样法从总体中抽取一个容量为5的样本，已知B层中的某个体甲被抽到的概率为，则总体中的个体数是____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

13．有下列数组排成一排：

如果把上述数组中的括号都去掉会形成一个数列：

有同学观察得到，据此，该数列中的第项是____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 5分

12.已知A、B、C是圆和三点，，____________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数单调性的应用

题型：填空题

分值: 5分

14．下图是一个几何体三视图，根据图中数据，计算该几何体的体积为___________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

指数函数的图像变换

题型：填空题

分值: 5分

15．下列命题正确的是____________。

①中，是为等腰三角形的充分不必要条件。

②的最大值为4

③函数是偶函数，则的图象关于直线对称

④已知在R上减，其图象过，则的解集是（-1，2）

⑤曲线所围成的图形的面积是2个平方单位。

正确答案

①②④⑤

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

简答题（综合题）本大题共75分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

16.已知.

（1）求的值;

（2）求的值。

正确答案

解：∵tanx=-2,且 ∴cosx=,sinx=-

（1）sinx-cosx=--=-

（2）原式= =

= =

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 12分

17．某人随机地将编号为1,2,3,4的四个小球放入编号为1,2,3,4的四个盒子中，每个盒子放一个小球，全部放完.

（1）求编号为奇数的小球放入到编号为奇数的盒子中的概率；

（2）当一个小球放到其中一个盒子时，若球的编号与盒子的编号相同时，称该球是“对”的，否则称该球是“放错”的，求至多有2个球“放对”的概率。

正确答案

（1）编号为奇数的小球放入到编号为奇数的盒子中,记为事件A

则P(A)=

（2）记至少有2个球“放对”为事件B,则P(B)=1-P()=1- =

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：简答题

分值: 12分

19.已知斜三棱柱在底面上的射影恰为的中点又；

（1）求证：平面；

（2）求斜三棱柱的侧面积。

正确答案

（1）∵A1在底面ABC上的射影为AC的中点D

∴平面A1ACC1⊥平面ABC∵BC⊥AC且平面A1ACC1∩平面ABC=AC

∴BC⊥平面A1ACC1 ∴BC⊥AC1

∵AC1⊥BA1且BC∩BA1=B ∴AC1⊥平面A1B

（2）斜三棱柱的侧面积为

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：简答题

分值: 12分

18.已知函数在点处的切线方程为．

（1）求函数的解析式；

（2）若经过点可以作出曲线的三条切线，求实数的取值范围。

正确答案

解：（1）．

根据题意，得即解得

所以．

（2）设切点为，则，，切线的斜率为

则=，即．

∵过点可作曲线的三条切线，

∴方程有三个不同的实数解，

∴函数有三个不同的零点，

∴的极大值为正、极小值为负

则．令，则或，列表：

由，解得实数的取值范围是．

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：简答题

分值: 14分

21．如图，已知抛物线的准线为,焦点为.⊙M的圆心在轴的正半轴上,且与轴相切．过原点作倾斜角为的直线,交于点, 交⊙M于另一点,且.

（Ⅰ）求⊙M和抛物线的方程；

（Ⅱ）若为抛物线上的动点,求的最小值；

（Ⅲ）过上的动点向⊙M作切线,切点为,求证：直线恒过一个定点,并求该定点的坐标。

正确答案

解：（Ⅰ）因为,即,所以抛物线C的方程为.

设⊙M的半径为,则,所以的方程为

（Ⅱ）设,则=

所以当时, 有最小值为2

（Ⅲ）以点Q这圆心,QS为半径作⊙Q,则线段ST即为⊙Q与⊙M的公共弦

设点,则,所以⊙Q的方程为

从而直线QS的方程为(*)

因为一定是方程(*)的解,所以直线QS恒过一个定点,且该定点坐标为

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值

题型：简答题

分值: 13分

20．在xoy平面上有一点列，点位于曲线（）上，以点为圆心的⊙与X轴都相切，且⊙与⊙又彼此外切，若，且（）。

（1）求证：数列是等差数列；

（2）设⊙的面积为，，求。

正确答案

解：（1）∵以点为圆心的⊙与X轴都相切，

∴⊙的半径

又∵⊙与⊙彼此外切，∴|⊙⊙|

∴

即

∵，∴

∴是以为首项，公差为2的等差数列。

（2）由（1）得

又

∴

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷