- 真题试卷
- 模拟试卷
- 预测试卷
2.下图给出4个幂函数的图象,则图象与函数的大致对应是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.若命题



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.设




①若


②若




③若


④若






其中真命题的序号是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.定义在






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知命题



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.将函数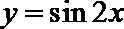
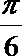
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
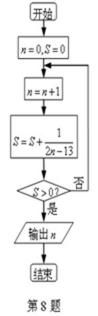
8.如图所示,输出的
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.将方程

①
②
③
④
其中,正确的判断是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.下列函数中,不满足
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
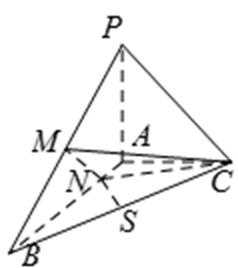
18.已知三棱锥PABC中,PA⊥平面ABC,AB⊥AC,PA=AC=AB,N为AB上一点,AB=4AN,M,S分别为PB,BC的中点.
(1)证明:CM⊥SN;
(2)求SN与平面CMN所成角的大小.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 已知向量


(1)若

(2)在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数


(1)当


(2)若

(3)当



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知


(1)求
(2)设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.设






(1)求函数
(2)若对于区间



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知关于x的二次函数
(1)设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数

(2)设点(a,b)是区域


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若方程


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.方程







正确答案
a<-6或a>6
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!