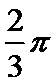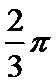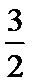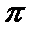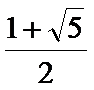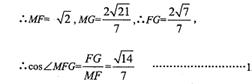- 真题试卷
- 模拟试卷
- 预测试卷
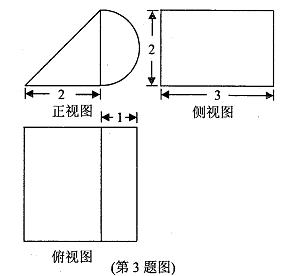
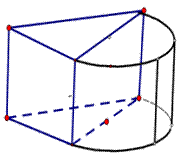
3.某几何体的三视图如图所示(单位:cm),则该几何体的体积等于( )cm3
正确答案
解析
将三视图画出直方图然后在旋转为立体图形。为三棱柱和半个圆柱。体积为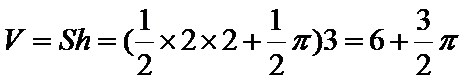
考查方向
解题思路
将三视图画出直方图然后在旋转为立体图形。
易错点
看成三棱锥,而出现错误。
知识点
4、函数(x)=sinx(sinx+
正确答案
解析
考查方向
解题思路
用三角函数倍角公式和辅助角公式进行化简,再结合三角函数的有界性进行求解即可。
易错点
辅助角公式的符合问题和特殊角问题。
知识点
5.已知a,b,c是正实数,则“b≤
正确答案
解析
解题思路
易错点
充要条件的判定和方法。
知识点
6.如图,将四边形ABCD中△ADC沿着AC翻折到ADlC,则翻折过程中线段DB中点M的轨迹是( )
正确答案
解析
考查方向
解题思路
过B作AC的垂线BE,过D作AC的垂线DF,连接DE,BF,然后证明在翻折过程中,BD中点到BE的中点的距离为定值得答案.
易错点
几何性质出现错误。
知识点
8.设函数f(x)= 
正确答案
解析
第1I卷
考查方向
解题思路
易错点
容易选择答案C,原因是条件问题。
知识点
1.直线x+(l-m)y+3=0(m为实数)恒过定点( )
正确答案
解析
考查方向
解题思路

易错点
选择答案D,错误原因是m=1
知识点
2.平面向量a=(1,x),b=(-2,3),若a∥b,则实数x的值为( )
正确答案
解析
考查方向
解题思路
根据平面向量的坐标表示与共线定理,列出方程求出x的值.
易错点
平行和垂直的条件问题混淆。
知识点
7.设等差数列{an}的前n项和为Sn,若数列{an}是单调递增数列,且满足a5≤6,S3≥9,则a6的取值范围是( )
正确答案
解析
解:∵数列{an}是单调递增数列,
若a5≤6,S3≥9,
∴a1+4d≤6 ①
3a1+3d≥9,即a1+d≥3 ②
∴(-1)×①+②,得
0<d≤1,
∴a6=a5+d,
∴3<a6=a5+d≤7
故选:D.
考查方向
解题思路
给出两个前n项和,写出求前n项和的公式,根据不等式的基本性质和等差数列的性质整理出结果.
易错点
隐含条件的挖掘。
知识点
9.计算,

正确答案
4,9.
解析

考查方向
解题思路
利用指数的运算和对数和指数的运算直接答案。
易错点

知识点
11.已知函数f(x)=Asin(2x+




正确答案
解析
考查方向
解题思路
根据三角函数的定义求出cosφ,得出φ;得出f(x)的解析式,利用正弦函数的单调性列出不等式解出
易错点
角
知识点
12.设a∈R,函数
正确答案
得a=-1,f(x)+3=0的解为-2。
解析
解:∵函数f(x)是奇函数,
∴f(0)=0,则20+a=1+a=0,得a=-1,
若x<0,则-x>0,
则f(-x)=2-x-1=-f(x),
则f(x)=1-2-x,x<0,
即g(x)=1-2-x,x<0,
由f(x)+3=0得f(x)=-3,
若x≥0,由f(x)=-3得2x-1=-3,得2x=-2,此时方程无解,
若x<0,由f(-x)=-3得1-2-x=-3,
得2-x=4,即-x=2,得x=-2,
故答案为:-2
考查方向
解题思路
根据函数奇偶性的性质建立方程关系进行求解即可.
易错点
奇函数的性质应用时候问题。
知识点
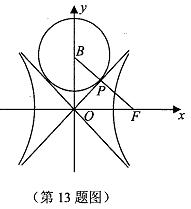
13.如图,双曲线C: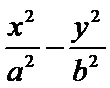
正确答案
解析
考查方向
解题思路
由题意BF垂直于双曲线的渐近线y=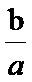
易错点
垂直的关系应用时候出现问题。
知识点
14.若实数x,y满足x+y-xy≥2,则|x-y|的最小值是 .
正确答案
2.
解析
考查方向
解题思路
易错点
线性规划问题的转换时候出现位置问题。
知识点
15.在△ABC中,BC=2,若对任意的实数t, |t





正确答案
8,
解析
考查方向
解题思路
由题意可得在线段BC上存在一点D,使得AD最小,且有AD⊥BC,取得最小值3,设BD=x,CD=2-x,运用勾股定理和向量数量积的定义和余弦定理,结合二次函数的最值的求法,即可得到最值.
易错点
在求最值时候构造函数问题。
知识点
10.若焦点在x轴上的椭圆的焦距为16,长轴长为18,则该椭圆的标准方程为__ .
正确答案
椭圆的标准方程为
解析
解题思路
易错点
长轴2a,不是a。
知识点
在△ABC中,内角A,B,C所对的边分别为a,b,c,c=2,A≠B.
16.求
17.若△ABC的面积为1,且tanC=2,求a+b的值.
正确答案
2
解析
考查方向
解题思路
利用正弦定理和余弦定理解决第一问,再利用余弦定理构造方程即可。
易错点
正弦定理的应用时候的转换余弦定理。
正确答案

解析
考查方向
解题思路
利用正弦定理和余弦定理解决第一问,再利用余弦定理构造方程即可。
易错点
正弦定理的应用时候的转换余弦定理。
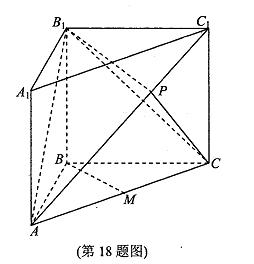
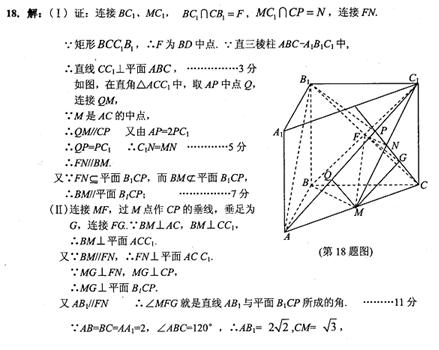
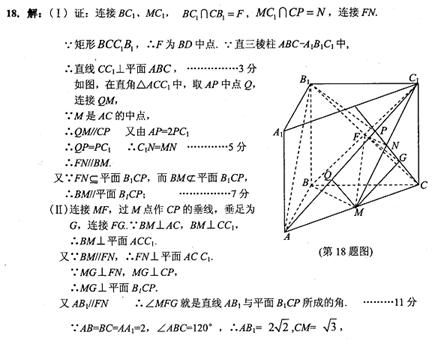
如图,在直三棱柱ABC-A1B1C1中,AB=BC=AAl=2,∠ABC=120°,点 P在线段AC1上,且AP=2PCl,M为线段AC的中点.
20.证明:BM//平面B1CP;
21.求直线AB1与平面B1CP所成角的余弦值。
正确答案
见解析
解析
考查方向
解题思路
利用线面平行判定定理证明线面平行,再利用射影定理确定角度,再求出角度。
易错点
建立空间直角坐标系的坐标问题。
正确答案
见解析
解析
考查方向
解题思路
利用线面平行判定定理证明线面平行,再利用射影定理确定角度,再求出角度。
易错点
建立空间直角坐标系的坐标问题。
设抛物线C:y2=2px(p>0)的焦点为F,点T(t,0)(t>0),且过点F的直线,交C于A,B.
22.当t=2时,若过T的直线交抛物线C于两点,且两交点的纵坐标乘积为-4,求焦点F的坐标;
23.如图,直线AT、 BT分别交抛物线C于点P、Q,连接PQ交x轴于点M,证明:|OF|,|OT|,|OM|成等比数列。
正确答案
见解析
解析
考查方向
解题思路
直线方程和抛物线方程方程联立,运用韦达定理,待定P的值,再利用几何性质解决实际问题。
易错点
解析几何最大的错误源于计算,所以容易出现计算错误。
正确答案
见解析
解析
考查方向
解题思路
直线方程和抛物线方程方程联立,运用韦达定理,待定P的值,再利用几何性质解决实际问题。
易错点
解析几何最大的错误源于计算,所以容易出现计算错误。
设函数f(x)=x2-ax,g(x)=|x-a|,其中a为实数.
24.若f(x)+g(x)是偶函数,求实数a的值;
25.设t∈R,若

正确答案
实数a的值0;实数t的最大值
解析
解题思路
易错点
分类讨论函数的时候出现丢解现象。
正确答案
实数a的值0;实数t的最大值
解析
解题思路
易错点
分类讨论函数的时候出现丢解现象。
已知数列{an}满足:a1=c,2an+1=an+l(c≠1,n∈N*),记数列{an}的前n项和为Sn.
18.令bn=an一l,证明:数列{bn}是等比数列;
19.求最小的实数c,使得对任意n∈N*,都有Sn≥3成立.
正确答案
见解析
解析
解题思路
易错点
数列{bn}的首项问题,求最小值时候的讨论。
正确答案
解析
解题思路
易错点
数列{bn}的首项问题,求最小值时候的讨论。