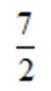- 真题试卷
- 模拟试卷
- 预测试卷
2.命题“

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知某几何体的侧视图与其正视图相同,相关的尺寸如下图所示,则这个几何体的体积是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知数列{



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.阅读右面的程序框图,运行相应的程序,则输出i的值为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知幂函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知A、B两点分别在两条互相垂直的直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.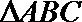



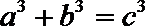
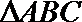
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.设函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.三棱锥ABCD中,E、H分别是AB、AD的中点,F、G分别是CB、CD的中点,若AC+BD=3,AC·BD=1,则EG2+FH2=__________
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
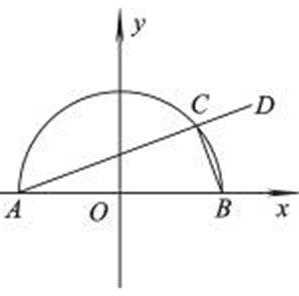
17.如图所示, C是

正确答案
圆;
解析
解析已在路上飞奔,马上就到!
知识点
11.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1—50号,并分组,第一组1—5号,第二组6—10号,……,第十组46—50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为__________的学生.
正确答案
37
解析
解析已在路上飞奔,马上就到!
知识点
12.在如图的表格中,每格填上一个数字后,使得每一横行成等差数列,每一纵列成等比数列,则
正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
13.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.过抛物线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.设x, y满足的约束条件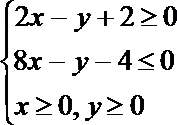
正确答案
4
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数
(1)求函数
(2)若

正确答案
(1)已知函数
∴
令
则
即函数
(2)由已知
∴ 当
解析
解析已在路上飞奔,马上就到!
知识点
19.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5。现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
(1)若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a,b,c的值;
(2)在(1)的条件下,将等级系数为4的3件日用品记为x1,x2,x3,等级系数为5的2件日用品记为y1,y2,现从x1,x2,x3,y1,y2这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率。
正确答案
(1)由频率分布表得a+0.2+0.45+b+c=1, a+b+c=0.35
因为抽取的20件日用品中,等级系数为4的恰有3件,所以b=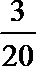
等级系数为5的恰有2件,所以c=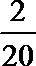
从而a=0.35-b-c=0.1
所以a=0.1 b=0.15 c=0.1
(2)从日用品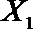
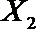
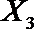
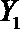
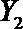
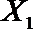
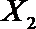
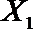

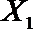
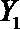
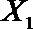
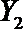
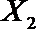
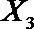
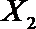
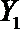
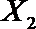
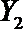
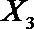
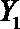
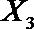
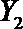
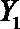
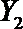
设事件A表示
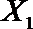
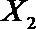
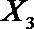
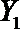
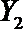
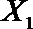
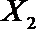
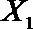
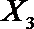
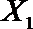
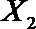
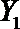
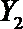
故所求的概率P(A)= 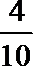
解析
解析已在路上飞奔,马上就到!
知识点
20.在如图所示的多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,且AC=AD=CD=DE=2,AB=1
(1)请在线段CE上找到点F的位置,使得恰有直线BF∥平面ACD,并证明这一事实;
(2)求多面体ABCDE的体积;
(3)求直线EC与平面ABED所成角的正弦值。
正确答案
(1)
如图,由已知AB⊥平面ACD,DE⊥平面ACD,
∴AB//ED,
设F为线段CE的中点,H是线段CD的中点,
连接FH,则

∴四边形ABFH是平行四边形,
∴
由


(2)取AD中点G,连接CG.
AB
∴CG
又CG
∴CG
∴



(3)连接EG,由(2)有CG
∴
设为

有
解析
解析已在路上飞奔,马上就到!
知识点
21.已知等差数列


(I)求数列

(II)设数列{








正确答案
(I)由已知得





又








(II)由



当n=1时,


当n>1时,



(1)-(2)得 











=1+2




解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)求函数
(2)若对于区间



(3)若过点


正确答案
(1)
根据题意,得
解得
(2)令
f(-1)=2, f(1)=-2,

则对于区间[-2,2]上任意两个自变量的值
所以

(3)设切点为



则
即
因为过点

所以方程
即函数
则
令


解析
解析已在路上飞奔,马上就到!