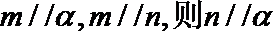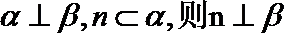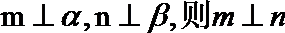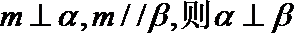文科数学济南市2011年高三试卷

精品

单选题
填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、单选题

2、填空题

3、简答题

真题试卷
模拟试卷
预测试卷

单选题本大题共12小题，每小题5分，共60分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

3．设m、n是两条不同的直线，α、β是两个不重合的平面，则下列命题中正确的是（）

A若

B若

C若

D若

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：单选题

分值: 5分

10．下列命题正确的是（）

A“a=2”是“直线平行于直线”的充分不必要条件

B“”是“”的必要不充分条件

C命题“若”的逆否命题为真命题

D命题“”的否定是：“”

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

四种命题及真假判断

题型：单选题

分值: 5分

1．复数Z满足，在复平面内，复数Z对应的点位于（）

A第一象限

B第二象限

C第三象限

D第四象限

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：单选题

分值: 5分

4．设，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：单选题

分值: 5分

5．一个正方体截去两个角后所得几何体的主视图、左视图如下图所示，则其俯视图为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：单选题

分值: 5分

6．函数的最小正周期和最大值分别为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 5分

7．若双曲线的左焦点在抛物线的准线上，则p的值为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程

题型：单选题

分值: 5分

8．一个袋中装有大小相同的4个红球，1个白球，从中随机取邮2个球，则取出的两个球不同色的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：单选题

分值: 5分

9．已知圆关于直线对称，则ab的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：单选题

分值: 5分

11．在等差数列中，首项，若，则k的值为（）

A15

B16

C17

D18

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：单选题

分值: 5分

12．已知函数的定义域为，部分对应值如下表，的图象如图所示，下列关于函数的命题：

①函数的值域为[0，2]；

②函数在区间[0，2]和[4，5]上是减函数；

③如果当时，的最大值是2，那么t的最大值为4；

④当有4个零点

其中真命题的个数是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的定义域及其求法

题型：单选题

分值: 5分

2．已知集合，中元素的个数有（）

A0个

B1个

C2个

D1个或2个

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

交集及其运算

填空题本大题共4小题，每小题4分，共16分。把答案填写在题中横线上。

题型：填空题

分值: 4分

13．如图，执行下图的程序框图，输出的T=_______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：填空题

分值: 4分

15．若圆相交于A，B两点，则|AB|=______。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

圆的标准方程

题型：填空题

分值: 4分

16．对于函数，若存在区间（其中），使得则称区间M为函数的一个“稳定区间”。

给出下列4个函数：

①

②

③

④

其中存在“稳定区间”的函数有______（填出所有满足条件的函数序号）

正确答案

①②③

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

14．已知，则=______。

正确答案

±2

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

18．在数列中，，若函数在点处切线过点

（1）求证：数列为等比数列；

（2）求数列的通项公式和前n项和公式

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 12分

17．在中，角A，B，C所对的边分别为a，b，c，且满足

（1）求；

（2）若，求a的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 12分

19．如图：C、D是以AB为直径的圆上两点（如图）AC=BC，F是AB上一点，且将圆沿直径AB折起，使点C在平面ABD的射影E在BD上，已知

（1）求证：平面BCE；

（2）求证：AD//平面CEF。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 12分

20．某地发生特大地震和海啸，使当地的自来水受到污染，某部门对水质检测后，决定往水中投放一种药剂来净化水质。已知每投放质量为m的药剂后，经过x天该药剂在水中释放的浓度y（毫克/升）满足，其中，当药剂在水中释放的浓度不低于4（毫克/升）时称为有效净化；当药剂在水中释放的浓度不低于4（毫克/升）且不高于10（毫克/升）时称为最佳净化。

（1）如果投放的药剂质量为m=6，试问自来水达到有效净化一共可持续几天？

（2）如果投放的药剂质量为m，为了使在6天（从投放药剂算起包括6天）之内的自来水达到最佳净化，试确定应该投放的药剂质量m的范围。

正确答案

（1）

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 12分

21．已知椭圆，其中短轴长和焦距相等，且过点

（1）求椭圆的标准方程；

（2）若在椭圆C的外部，过P做椭圆的两条切线PM、PN，其中M、N为切点，则MN的方程为已知点P在直线上，试求椭圆右焦点F到直线MN的距离的最大值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：简答题

分值: 14分

22．已知函数，其定义域为

（1）试确定t的范围，使得函数在区间[-2，t]上为增函数；

（2）求证：

（3）求证：对任意总有满足，并确定这样的的个数。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷