- 真题试卷
- 模拟试卷
- 预测试卷
4.“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知实数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.用反证法证明命题:“已知a,b∈N,若ab不能被7整除,则a与b都不能被7整除”时,假设的内容应为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.执行如图所示的程序框图,若输出值

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在△ABC中,内角A,B,C的对边分别为a,b,c.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.已知△ABC中,AB=1,AC=2,O为△ABC的外心,则

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.设等比数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知幂函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知以


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在下列给出的命题中,
①函数

②对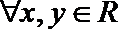

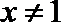
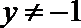
③若实数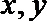



④若

⑤把函数


其中正确结论的序号是__________。
正确答案
①②③
解析
解析已在路上飞奔,马上就到!
知识点
16.定义在R上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是


(1)求x∈
(2)求函数f(x)的单增区间。
正确答案
解:
(2)当


所以

当


有函数的周期性知所以

解析
解析已在路上飞奔,马上就到!
知识点
17.在甲、乙两个盒子中分别装有编号为1,2,3,4的四个形状相同的小球,现从甲、乙两个盒子中各取出2个小球,每个小球被取出的可能性相等.
(1)求从甲盒中取出的两个球上的编号不都是奇数的概率;
(2)求从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等的概率。
正确答案
解:由题意可知,从甲.乙两个盒子中各取1个小球的基本事件总数为16.
(1)记“从甲盒中取出的两个球上的编号不都是奇数”为事件

(1,,2),(1,4),(2,3),(2,4),(3,4)共5个.
(2) 记“从甲盒取出的小球上编号之和与从乙盒中取出的小球上编号之和相等”为事件
则事件
(12,12),(13,13),(14,14),(14,23),(23,14),(23,23),(24,24)(34,34)共8个基本事件
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,平面





(1)求证:

(2)当


正确答案
(1)证明:由

且在△APE中,

又依题意

因为



所以

(2)解:由已知平面


在等边三角形PAC中,


解析
解析已在路上飞奔,马上就到!
知识点
19.设数列


(1)证明:数列
(2)求数列


正确答案
(1)
又
所以数列
(2)由(1)知

设
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:



(1)求椭圆C的方程;
(2)设






正确答案
解:(1)椭圆


所以所求椭圆
(2)设




由

所以直线

解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)当



(2)求函数
正确答案
解:(1)当


所以

所以曲线


(2)函数

①当




所以


②当




所




③当



所以

④当




所以



解析
解析已在路上飞奔,马上就到!







































































