文科数学浦东新区2013年高三试卷

精品

填空题
简答题
单选题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、简答题

3、单选题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

2．若，则（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

二次函数的应用

题型：填空题

分值: 4分

4．函数的单调递减区间是（）。

正确答案

（2，+∞）

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

6．若展开式中常数项等于（）。

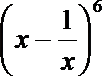
正确答案

-20

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：填空题

分值: 4分

3．若的反函数，则（）。

正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

12．已知函数，，则函数的值域为（）。

正确答案

[2，3]

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

10．已知函数定义域为是偶函数，则函数的值域为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

1．已知全集，，，则=（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：填空题

分值: 4分

8．定义在上的函数既是偶函数又是周期函数，若的最小正周期为，且当时，，则的值是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

9．旅游公司为3个旅游团提供4条旅游线路，每个旅游团任选其中一条. 则3个旅游团选择3条不同的线路的概率（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法

题型：填空题

分值: 4分

11．方程的解为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：填空题

分值: 4分

13．设函数在内有定义，对于给定的正数K，定义函数

取函数。当=时，函数的单调递增区间为（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 4分

14．已知函数

①；

②；

③；

④

其中对于定义域内的任意一个自变量，都存在定义域内的唯一一个自变量，使得成立的函数是（）。

正确答案

③

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 4分

5．函数的最小正周期是（）。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

三角函数的周期性及其求法三角函数中的恒等变换应用

题型：填空题

分值: 4分

7．设函数，则实数的取值范围是（）。

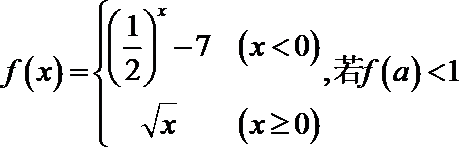
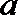
正确答案

（-3，1）

解析

解析已在路上飞奔，马上就到！

知识点

其它不等式的解法

简答题（综合题）本大题共78分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 12分

19．解不等式：．

正确答案

原不等式变形为，

所以，原不等式可化为

即：

故原不等式解集为{x|2<x<3}

解析

解析已在路上飞奔，马上就到！

知识点

函数的值域及其求法

题型：简答题

分值: 14分

20．在中，是角所对的边，是该三角形的面积，且

（1）求角；

（2）若，求的值

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：简答题

分值: 18分

22．已知函数．

（1）求满足的值；

（2）写出函数的单调递增区间；

（3）若函数,求函数的值域。

正确答案

（1）

当时，由，得x>2

当时，由无解。

所以，不等式的解集为

（2）由，

当时，的单调递增区间为；

当时，的单调递增区间为。

所以，的单调递增区间是。

（3）设

因为，所以即

因为，所以，

所以即

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 16分

21．为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层．某幢建筑物要建造可使用20年的隔热层，每厘米厚的隔热层建造成本为6万元．该建筑物每年的能源消耗费用C（单位：万元）与隔热层厚度（单位：cm）满足关系：，若不建隔热层，每年能源消耗费用为8万元．设为隔热层建造费用与20年的能源消耗费用之和．

（1）求的值及的表达式；

（2）隔热层修建多厚对时，总费用达到最小，并求最小值．

正确答案

（1）

（2）

当且仅当即时，有最小值70万元。

答：隔热层修建5cm时，总费用达到最小，最小值为70万元。

解析

解析已在路上飞奔，马上就到！

知识点

函数解析式的求解及常用方法

题型：简答题

分值: 18分

23．对于函数，如果存在实数使得，那么称为的生成函数.

（1）下面给出两组函数，是否分别为的生成函数？并说明理由；

第一组：；

第二组：；

（2）设，生成函数.若不等式

在上有解，求实数的取值范围；

（3）设，取，生成函数使恒成立，求的取值范围。

正确答案

（1）①设，

取，所以是的生成函数。

② 设，即，

则，该方程组无解，所以不是的生成函数。

（2）

若不等式在[2，4]上有解，

，即

（3）由题意，得

1°若，则在上递减，在上递增，

则，所以，得

2°若，则在[1，10]上递增，则，

所以，得。

3°若，则在[1，10]上递增，则，

故,无解

综上可知，

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

单选题本大题共4小题，每小题4分，共16分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 4分

15．“”是“不等式成立”的（）

A充分非必要条件

B必要非充分条件

C充要条件

D既非充分亦非必要条件

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

必要条件

题型：单选题

分值: 4分

16．设集合，集合，且，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义

题型：单选题

分值: 4分

18．对于方程，下列说法错误的是（）

A该方程没有大于0的实数解

B该方程有无数个实数解

C该方程在内有且只有一个实数解

D若是该方程的实数解，则

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：单选题

分值: 4分

17．在下列函数中，既是上的增函数，又是以为最小正周期的偶函数的函数是（）

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷