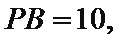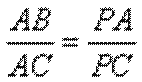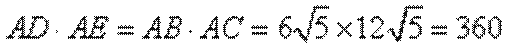- 真题试卷
- 模拟试卷
- 预测试卷
2.已知命题P:∀x∈R,ex﹣x﹣1>0,则¬P是( )
正确答案
解析
由全称命题的否定为存在性命题可知命题p的否定为∃x0∈R,ex0﹣x0﹣1≤0,故选择C选项。
考查方向
解题思路
由全称命题的否定为存在性命题可知选择B选项。
易错点
忘记命题的否定只否结论不否条件导致出错。
知识点
5.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
正确答案
解析
易知,该几何体的原图为ABDB1D1,如下图所示,
故其体积为

考查方向
解题思路
先由三视图还原几何体,再根据几何体的形状求其体积。
易错点
不能由三视图还原实物图导致出错。
知识点
1.已知集合A={1,2},B={1,m,3},如果A∩B=A,那么实数m等于( )
正确答案
解析
由A∩B=A知
考查方向
解题思路
由A∩B=A知
易错点
对A∩B=A等价于
知识点
6.已知


正确答案
解析
由








考查方向
解题思路
先由


易错点
三角函数性质不熟悉导致出错。
知识点
7.已知等比数列{an}中,各项都是正数,且3a1,

正确答案
解析
由3a1,





考查方向
解题思路
先由3a1,

易错点
等比数列相关性质不熟悉导致出错。
知识点
11.气象意义上从春季进入夏季的标志为:“连续5天的日平均温度均不低于22 (℃)”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区有( )
正确答案
解析
甲地:5个数据的中位数为24,众数为22,根据数据得出:甲地连续5天的日平均温度记录数据可能为:22,22,24,25,26,其连续5天的日平均温度均不低于22;乙地:5个数据的中位数为27,总体均值为24,当5个数据为19,20,27,27,27可知其连续5天的日平均温度有低于22,故不正确;丙地:5个数据中有一个数据是32,总体均值为26,若有低于22,则取21,此时方差超出了10.8,可知其连续5天的日平均温度均不低于22.则肯定进入夏季的地区有甲、丙两地,故选择C选项。
考查方向
解题思路
利用相关概念逐一进行判断。
易错点
相关概念不熟悉导致出错。
知识点
3.已知复数z,“z+
正确答案
解析
设复数z的代数形式为z=a+bi(a,b∈R)由z+




考查方向
解题思路
设出复数z的代数形式,由z+
易错点
对纯虚数的概念不熟悉错导致出错。
知识点
4.执行如图所示的程序框图,若输出的S为4,则输入的x应为( )
正确答案
解析
若


考查方向
解题思路
根据条件框中的条件及输出的S值即可求出x的值。
易错点
对条件语句的判断失误导致出错。
知识点
9.已知不等式组
正确答案
解析
该不等式组表示的平面区域如下图所示,则其面积
考查方向
解题思路
由不等式组所表示的平面区域的面积为4即可求出k。
易错点
对题中所给条件不知如何应用导致出错。
知识点
10.已知正实数m,n满足:m+n=1,且使



正确答案
解析
由:m+n=1知





考查方向
解题思路
先由均值不等式求出m的值,再求
易错点
均值不等式不会用导致出错。
知识点
12.设f′(x)是函数f(x)的导函数,且

正确答案
解析
令












考查方向
解题思路
构造函数
易错点
不能利用导数构造出函数导致出错。
知识点
8.函数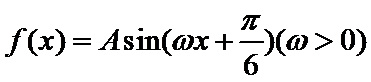
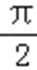
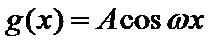
正确答案
解析
由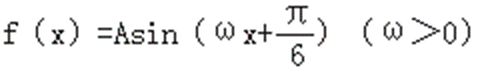
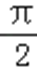
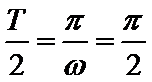
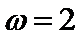
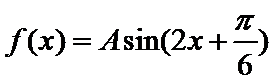
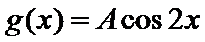
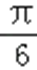
考查方向
解题思路
先由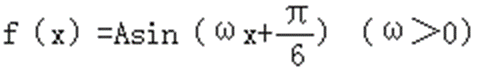
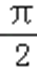
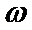
易错点
三角函数图像变换公式不熟导致出错。
知识点
14.若非零向量














正确答案
解析
试题分析:设






























考查方向
解题思路
由








易错点
对题所给条件不知如何应用导致本题没有思路。
知识点
15.在平面直角坐标系中,△ABC的顶点A、B分别是离心率为e的圆锥曲线
正确答案
解析
试题分析:设三角形△ABC中角A,B,C的对边分别为a,b,c,则因为△ABC的顶点A、B分别是离心率为e的圆锥曲线





考查方向
解题思路
由类比推理的概念及正弦定理即可解决本题。
易错点
对题意不理解导致本题没有思路。
知识点
13.若数a1,a2,a3,a4,a5的标准差为2,则数3a1﹣2,3a2﹣2,3a3﹣2,3a4﹣2,3a5﹣2的方差为 .
正确答案
36
解析
试题分析:因为a1,a2,a3,a4,a5的标准差为2,所以其方差为4,设数据a1,a2,a3,a4,a5的平均数为



考查方向
解题思路
根据标准差求出方差,再利用均值与方差的性质求出所给数据的方差。
易错点
对方差与标准差的概念不清楚导致出错。
知识点
16.对于函数y=f(x),若存在定义域D内某个区间[a,b],使得y=f(x)在[a,b]上的值域也为[a,b],则称函数y=f(x)在定义域D上封闭,如果函数f(x)=﹣
正确答案
6
解析
试题分析:因为f(x)=﹣





















考查方向
解题思路
先判断奇偶性,再判断单调性,解方程f(a)=b,f(b)=a。即可
易错点
新概念不易理解。
知识点
17.某校为了解学生的视力情况,随机抽查了一部分学生视力,将调查结果分组,分组区间为(3.9,4.2],(4.2,4.5],…,(5.1,5.4].经过数据处理,得到如下频率分布表:
(Ⅰ)求频率分布表中未知量n,x,y,z的值;
(Ⅱ)从样本中视力在(3.9,4.2]和(5.1,5.4]的所有同学中随机抽取两人,求两人的视力差的绝对值低于0.5的概率.
正确答案
(1)n=50,x=50,y14,z=0.28;(2)
解析
试题分析:本题属于用样本估计总体与古典概型综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(I)由表可知,样本容量为n,
由(5.1,5.4]一组频数为2,频率为0.04,则
由
y=50﹣3﹣6﹣25﹣2=14,
(II)设样本视力在(3.9,4.2]的3人为a,b,c;样本视力在(5.1,5.4]的2人为d,e.
由题意从5人中任取两人的基本事件空间为:Ω={(a,d),(a,e),(b,d),(b,e),(c,d),(c,e),(a,b),(a,c),(b,c),(d,e)},共10个基本事件;
设事件A表示“抽取的两人的视力差的绝对值低于0.5”,则事件A包含的基本事件有:(a,b),(a,c),(b,c),(d,e),共4个基本事件;
P(A)=

故抽取的两人的视力差的绝对值低于0.5的概率为
考查方向
解题思路
(1)由表中数据求解;
(2)根据古典概型求解.
易错点
相关知识点不熟容易处错。
知识点
18.在直三棱柱ABC﹣A1B1C1中,AB=AC=AA1=3,BC=2,D是BC的中点,F是C1C上一点.
(1)当CF=2,求证:B1F⊥平面ADF;
(2)若FD⊥B1D,求三棱锥B1﹣ADF体积.
正确答案
(1)见证明;(2)
解析
试题分析:本题属于立体几何的综合应用问题,属于中档题,只要掌握相关立体几何的知识,即可解决本题,解析如下:
(1)证明:∵AB=AC,D是BC的中点,
∴AD⊥BC.在直三棱柱ABC﹣A1B1C1中,
∵B1B⊥底面ABC,AD⊂底面ABC,∴AD⊥B1B.
∵BC∩B1B=B,∴AD⊥平面B1BCC1.
∵B1F⊂平面B1BCC1,∴AD⊥B1F.
在矩形B1BCC1中,∵C1F=CD=1,B1C1=CF=2,
∴Rt△DCF≌Rt△FC1B1.
∴∠CFD=∠C1B1F.∴∠B1FD=90°,∴B1F⊥FD.
∵AD∩FD=D,∴B1F⊥平面ADF.
(2)解:∵AD⊥面B1DF,
又
∵FD⊥B1D,∴Rt△CDF∽Rt△BB1D,∴
∴
∴
考查方向
解题思路
(1)利用相关定理进行证明;
(2)利用等体积法即可求解.
易错点
相关定理不熟容易处错。
知识点
20.如图,F是椭圆



(1)求该椭圆的标准方程;
(2)若直线l与上下半椭圆分别交于点P、Q,与x轴交于点M,且|PM|=2|MQ|,求△OPQ的面积取得最大值时直线l的方程.
正确答案
(1)




解析
试题分析:本题属于圆锥曲线的综合应用问题,属于拔高题,不容易得分,解析如下:
(1)由题意可得c=
将x=c代入椭圆方程可得y=±b

即有△OP0Q0的面积为

即



(2)设M(t,0),且
直线PQ:x=my+t,代入椭圆方程,
可得(4m2+9)y2+8mty+4t2﹣36=0,
设P(x1,y1),Q(x2,y2),y1+y2=﹣

由|PM|=2|MQ|,可得

t2=

则△OPQ的面积为S=

=6|t|•

当t2=5<9,此时m2=

故所求直线方程为x=±



考查方向
解题思路
(1)利用相关知识求椭圆方程;
(2)联立方程组,由|PM|=2|MQ|找关系,整理即可求解.
易错点
对题中条件的处理容易出错。
知识点
21.设函数f(x)=c lnx+
(Ⅰ)若x=1为f(x)的极大值点,求f(x)的单调区间(用c表示);
(Ⅱ)若f(x)=0恰有两解,求实数c的取值范围.
正确答案
(1)见解析;(2)
解析
试题分析:本题属于导数的综合应用问题,属于拔高题,不容易得分,解析如下:

∵x=1为f(x)的极值点,∴f'(1)=0,
∴
(I)若x=1为f(x)的极大值点,
∴c>1,当0<x<1时,f'(x)>0;当1<x<c时,f'(x)<0;
当x>c时,f'(x)>0.∴f(x)的递增区间为(0,1),(c,+∞);递减区间为(1,c).
(II)①若c<0,则f(x)在(0,1)上递减,在(1,+∞)上递增,
f(x)=0恰有两解,则f(1)<0,即

②若0<c<1,则f(x)的极大值为f(c)=clnc+
f
则

f
③若c>1,则


综上,使f(x)=0恰有两解的c的范围为: 
考查方向
解题思路
(1)先由1为极值点求出b+c+1=0,再有导数范围求单调区间;
(2)更具参数c的范围进行讨论.
易错点
第二问对题中所给条件不知如何下手导致失分。
知识点
19.设a、b、c分别是△ABC三个内角∠A、∠B、∠C的对边,若向量


(1)求tanA•tanB的值;
(2)求
正确答案
(1)

解析
试题分析:本题属于向量与三角函数的综合应用问题,属于简单题,只要掌握相关的知识,即可解决本题,解析如下:
(1)由
即 
亦即 4cos(A﹣B)=5cos(A+B)
所以
(2)因
而
所以,tan(A+B)有最小值

又tanC=﹣tan(A+B),则tanC有最大值

考查方向
解题思路
(1)由向量数量积的坐标运算公式直接计算;
(2)利用两角和的正切公式及均值不等式进行计算。
易错点
相关知识点不熟容易处错。
知识点
22.选修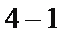
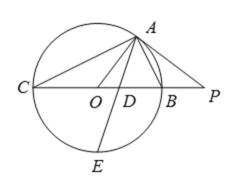
如图所示,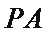

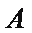


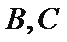
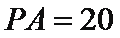



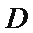
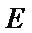
(Ⅰ)求证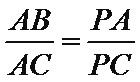
(Ⅱ)求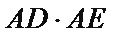
正确答案
(1)见解析;(2)
解析
试题分析:本题属于圆的综合应用问题,属于简单题,只要掌握相关圆的知识,即可解决本题,解析如下:
(1)由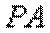
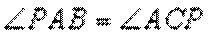
又
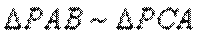
(2)由
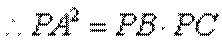
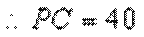
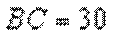
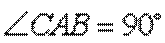
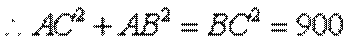
又由(1)知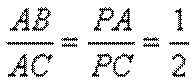
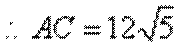
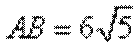
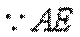
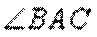
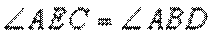
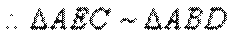
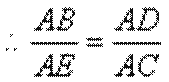
考查方向
解题思路
(1)利用相似三角形即可得证;
(2)利用切割线定理即可求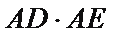
易错点
相关定理不熟悉导致本题失分。