- 真题试卷
- 模拟试卷
- 预测试卷
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知



正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
3.为了解今年某校高三毕业班准备报考飞行员学生的体重(单位:kg)情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为
正确答案
48
解析
解析已在路上飞奔,马上就到!
知识点
4.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知双曲线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.正四面体







正确答案
1
解析
解析已在路上飞奔,马上就到!
知识点
7.已知

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.下图给出了一个程序框图,其作用是输入x的值,输出相应的y值。若要使输入的x值与输出的y值相等,则这样的x值有( )个。
正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
9.在









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知椭圆






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.若不等式组

正确答案

解析
解析已在路上飞奔,马上就到!
知识点
13.若曲线





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.如图,某小区有一边长为2(单位:百米)的正方形地块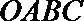
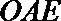
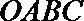
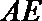
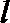
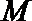
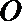
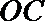
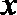
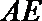
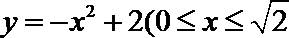
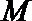
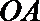
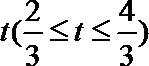
(1)当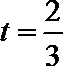
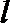
(2)当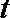
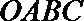
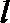
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.对于数列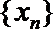
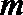
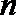
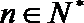
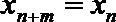
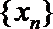
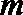
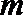
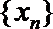
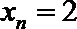
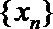
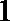
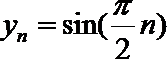
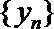
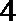
(Ⅰ)设数列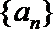
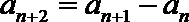
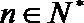
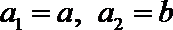
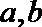
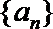
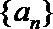
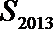
(Ⅱ)设数列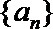
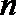
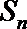
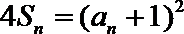
①若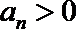
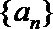
②若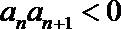
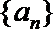
(Ⅲ)设数列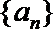
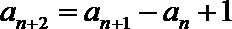
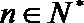
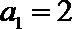
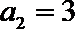
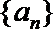
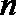
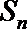
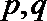
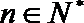
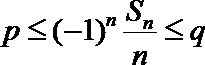
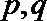
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.如图,椭圆的中心在坐标原点,长轴端点为



(1) 求椭圆的标准方程;
(2) 过椭圆的右焦点







①证明:
②求四边形

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数









(Ⅰ)已知函数



(Ⅱ)已知


求证:
(Ⅲ)定义集合





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.如图,在四棱锥










求证:
(1)

(2)

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如图,四边形






(1)证明:
(2)若




正确答案
解析
解析已在路上飞奔,马上就到!

































