- 真题试卷
- 模拟试卷
- 预测试卷
4.函数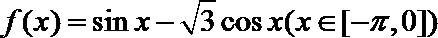
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.正数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设等差数列




正确答案
3
解析
解析已在路上飞奔,马上就到!
知识点
5.已知




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 含有三个实数的集合可表示为

正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
6.集合
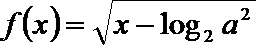
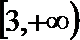
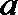
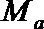
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知圆锥的底面半径


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若经过点P(-1,0)的直线与圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个的编号与座位号一致的坐法是_______。
正确答案
20
解析
解析已在路上飞奔,马上就到!
知识点
2.若行列式

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.如下图所示的程序框图的输出结果是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数

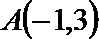
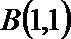

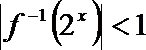
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.用数学归纳法证明1–







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.四棱柱成为平行六面体的充分不必要条件是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.在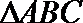



(1)求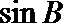
(2)若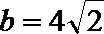
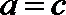
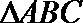
正确答案
(1)由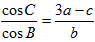

即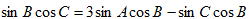
∴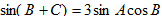

∵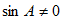
∴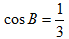
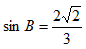
(2)∵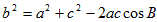
32=
∵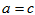
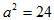
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数

(1)确定实数


(2)确定实数




(3)如果


正确答案
(1)方程

令

故0<
(2)又
∴
由于-






依题意



因此,若


(3)如果M为真命题,且N 为假命题,则
如果N为真命题,且M为假命题,则
故

解析
解析已在路上飞奔,马上就到!
知识点
22.已知二次曲线Ck的方程:
(1)分别求出方程表示椭圆和双曲线的条件;
(2)若双曲线Ck与直线
正确答案
(1)当且仅当

当且仅当

(2)解法一:由


∵双曲线实轴最长,
∴

此时双曲线方程为
解法二:若


联立

∵

∴

∴实轴最长的双曲线方程为
解法三:不妨先求得


设直线与双曲线左支交点为M,则
∴
∴实轴最长的双曲线方程为
解法四:设双曲线与直线公共点为
则

∴
∴
∴实轴最长的双曲线方程为
解析
解析已在路上飞奔,马上就到!
知识点
20.如图所示,已知单位正方体


(1)求
(2)求异面直线

正确答案
(1)过E作EF⊥平面ABCD,F为垂足,
∴AF是AE在底面ABCD上的射影,
∴∠EAF就是求AE与下底面所成角的大小,
∴在Rt△EAF中,∠EAF=arctan
因此,AE与下底面所成角的大小为arctan
(2)∵EF//CC'//DD',∴∠AEF就是异面直线AE与DD'所成的角,
∴在Rt△EAF中,∠AEF=arctan
因此,AE与DD'所成角的大小为acrtan
解析
解析已在路上飞奔,马上就到!
知识点
23.由函数










(1)若函数



(2)已知正数数列



(3)在(1)和(2)的条件下,







正确答案
解析
解析已在路上飞奔,马上就到!