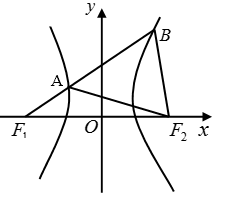
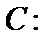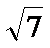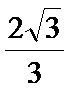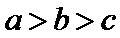- 真题试卷
- 模拟试卷
- 预测试卷
在△ABC中,设内角


16.求角C;
17.若

正确答案
见解析
解析
因为

因为在△ABC中,
所以
考查方向
解题思路
第1问,根据条件化简整理可得角C,第二问,利用余弦定理求面积
易错点
正弦定理、余弦定理的性质掌握不好
正确答案
见解析
解析
因为
所以
因为
所以
所以
所以
所以
考查方向
解题思路
第1问,根据条件化简整理可得角C,第二问,利用余弦定理求面积
易错点
正弦定理、余弦定理的性质掌握不好
如图,在四棱锥








18.求证:

19.求证: 
20.求

正确答案
见解析
解析
连结
















考查方向
解题思路
通过线线平行证明线面平行,
易错点
找不到二面角,辅助线作不出来
正确答案
见解析
解析













考查方向
解题思路
通过面面垂直证明线线垂直。
易错点
找不到二面角,辅助线作不出来
正确答案
见解析
解析
过F作




又












考查方向
解题思路
第1问通过线线平行证明线面平行,
第2问通过面面垂直证明线线垂直。
第3问,找到二面角构造三角形,利用余弦定理求解
易错点
找不到二面角,辅助线作不出来
设数列







21.求数列

22.设




正确答案
见解析
解析
由已知条件得
当
当

①-②得:
即

又

∵
∴

考查方向
解题思路
第1问,根据Sn求an,第2问,构造适当的数列,裂项相消,得到证明结论。
易错点
相关公式记错,不会构造数列
正确答案
见解析
解析
∵
∴ 

两式相减得

考查方向
解题思路
第1问,根据Sn求an,第2问,构造适当的数列,裂项相消,得到证明结论。
易错点
相关公式记错,不会构造数列
椭圆C:


23.求椭圆C的方程 ;
24.设椭圆C的两焦点分别为



25.若直线





正确答案
见解析
解析


又

椭圆
考查方向
解题思路
第1问,利用椭圆的概念与所给的离心率,求出a和b的值,进而得到椭圆C的方程,第2问,求出圆的半径与圆心坐标即可,第3问,将直线方程和椭圆方程联立,求出交点坐标。然后判断交点是否在直线上。
易错点
计算能力
正确答案
见解析
解析

所以











考查方向
解题思路
第1问,利用椭圆的概念与所给的离心率,求出a和b的值,进而得到椭圆C的方程,第2问,求出圆的半径与圆心坐标即可,第3问,将直线方程和椭圆方程联立,求出交点坐标。然后判断交点是否在直线上。
易错点
计算能力
正确答案
见解析
解析
将直线


得






由根与系数的关系,得
直线

它与直线
同理可求得直线


下面证明
即证明


因此结论成立.
综上可知.直线


考查方向
解题思路
第1问,利用椭圆的概念与所给的离心率,求出a和b的值,进而得到椭圆C的方程,第2问,求出圆的半径与圆心坐标即可,第3问,将直线方程和椭圆方程联立,求出交点坐标。然后判断交点是否在直线上。
易错点
计算能力
已知函数
26.求函数
27.若不等式


28.求证:
正确答案
见解析
解析
∵ 
∴ 
令
故函数
考查方向
解题思路
确定函数的定义域,利用导数求函数的单调性区间,根据题意构造出恰当的函数,利用函数与不等式之间的关系,证明结论。
易错点
求导错误,没有构造出适合的函数
正确答案
见解析
解析
由
则问题转化为

又 
令 




由表知当
函数

因此
考查方向
解题思路
确定函数的定义域,利用导数求函数的单调性区间,根据题意构造出恰当的函数,利用函数与不等式之间的关系,证明结论。
易错点
求导错误,没有构造出适合的函数
正确答案
见解析
解析
由(Ⅱ)知
∴ 

∴
又∵

考查方向
解题思路
确定函数的定义域,利用导数求函数的单调性区间,根据题意构造出恰当的函数,利用函数与不等式之间的关系,证明结论。
易错点
求导错误,没有构造出适合的函数
1. 已知全集U=



正确答案
解析
因为



考查方向
解题思路
根据补集和并集的概念,求解
易错点
混淆概念
知识点
3. 阅读右面的程序框图,当程序运行后,输出
正确答案
解析
s=1,k=1K=2,s=4,k=2不满足判断框中的条件K=3,S=11,K=3 不满足判断框中的条件K=4,S=26,K=4 不满足判断框中的条K=5,S=57,K=5 不满足判断框中的条件K=6,S=120,K=6 满足判断框中的条件,输出S=120,所以选C
考查方向
解题思路
顺序结构,循环结构,判断结构
易错点
循环语句理解错误,判断条件看错
知识点
4. 设实数

有实根的概率为( )
正确答案
解析
因为
所以
解得
记事件A:P在[0,5]上随机地取值,
关于x的方程
由方程
所以
考查方向
解题思路
先求出p的取值范围,然后用几何概型求概率
易错点
不用几何概型建模
知识点
6. 将

正确答案
解析
因为将

得到
所以
即
所以选A
考查方向
解题思路
先平移,再化简
易错点
平移后没有化简整理,找不到选项
知识点
2. “

正确答案
解析





考查方向
解题思路
先解绝对值不等式,然后判断逻辑关系
易错点
充分条件和必要条件理解有误,解绝对值不等式解错
知识点
如图,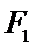
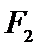
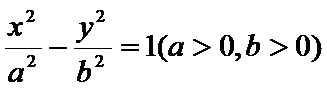
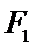
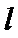
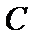
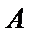
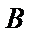
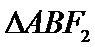
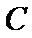
正确答案
解析
因为A、B是双曲线上的点
所以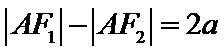
因为是等边三角形,
所以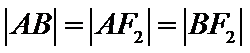
所以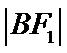
所以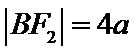
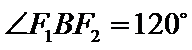
所以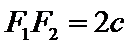
所以根据余弦定理,
可得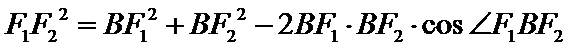
将数据代入得,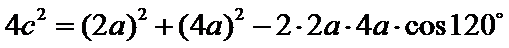
整理得,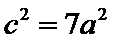
所以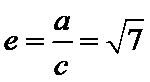
所以选B
考查方向
解题思路
利用双曲线的性质,结合余弦定理求解
易错点
计算能力,想不到利用余弦定理
知识点
8. 设函数
在


正确答案
解析
如图所示,
由题意可知,
可以令
即是

由此可以得到参数

所以选C
考查方向
解题思路
作出正确的图象,找到临界值
易错点
不能做出正确的图象,不理解函数零点的意思
知识点
5. 若
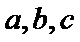
正确答案
解析
因为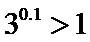

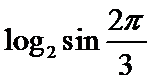
所以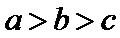
考查方向
解题思路
找到中间值(和1做比较)
易错点
找不到中间值,做比较
知识点
12.



且

正确答案
8
解析


所以

所以

所以填8
考查方向
解题思路
先求出a7的值,然后再求答案
易错点
不转换建立关系,直接算
知识点
13. 已知实数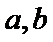
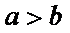
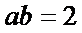
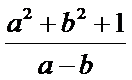
正确答案
解析
因为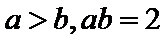
所以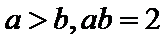
因为
所以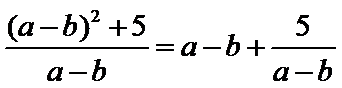
因为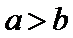
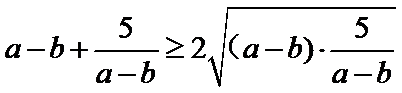
所以最小值为
考查方向
解题思路
先化简成基本不等式情况,然后再利用不等式性质求
易错点
想不到利用基本不等式,而是利用二次函数求最值
知识点
9. 已知




正确答案
解析
因为
所以
考查方向
解题思路
利用复数的四则运算计算
易错点
计算错误,虚数单位理解错误
知识点
10. 已知一个空间几何体的三视图如下图所示,则该几何体的体积为 cm3.
正确答案
解析
由三视图可得,
几何体是一个圆柱中间挖去一个半球得到的几何体,
先求圆柱体体积
半球的体积
所以几何体的体积为
考查方向
解题思路
根据三视图,还原成空间几何体,并注意相关线段的长度
易错点
从三视图还原成空间几何体错误
知识点
11. 如下图,





则
正确答案
解析


所以
设

求得,
由勾股定理可得,

所以
所以
考查方向
解题思路
根据切线长定理,勾股定理求解
易错点
圆中线段关系弄错
知识点
14. 已知菱形









正确答案
解析
因为ABCD是菱形,
向量AE和向量AF的积为1,
所以AB=BC=CD=DA=2,
因为向量DC等于2倍的向量DF,
所以DF=1,即F为CD的中点,
E是BC的三等分点,
因为BE和CE的方向相反,
所以
考查方向
解题思路
根据已知条件,用含有
易错点
向量是有方向的,相反方向为负值,常常会被忽略
知识点
15.某厂用甲、乙两种原料生产A、B两种产品,已知生产1吨A产品,1吨B产品分别需要
的甲、乙原料数,每种产品可获得的利润数及该厂现有原料数如下表所示.
问:在现有原料下,A、B产品应各生产多少吨才能使利润总额最大?
利润总额最大是多少万元?
正确答案
见解析
解析
设生产A、B产品分别为x,y吨,利润总额为z元, 由题意得 目标函数为z=7x+12y. 作出二元一次不等式组所表示的平面区域,即可行域,
如图:
目标函数可变形为
∴当


解得
将点A(20,24)代入z=7x+12y
得zmax=7×20+12×24=428万元.
答:该厂生产A,B两种产品分别为20吨、24吨时利润最大,最大利润为428万元.
考查方向
解题思路
根据题意,根据所给表格里的条件,找到目标函数和可行域,根据线性规划性质求解。
易错点
找不到约束条件和目标函数