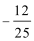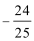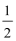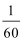- 真题试卷
- 模拟试卷
- 预测试卷
1.设不等式




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.把函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.若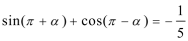
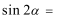
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知
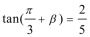

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知命题



正确答案
(0,1)
解析
解析已在路上飞奔,马上就到!
知识点
15.给出下列命题:
①

②若

③在


④在


其中正确命题的序号为( )。
正确答案
①②
解析
解析已在路上飞奔,马上就到!
知识点
12.已知

正确答案
2008
解析
解析已在路上飞奔,马上就到!
知识点
13.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.


(1)求角
(2)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数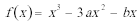
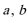
(1)若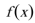
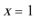
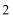
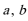
(2)若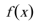
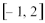
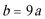
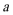
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数
(1)求
(2)将




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数

(1)求
(2)不等式




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.某工厂统计资料显示,产品次品率


又知每生产一件正品盈利


(1)将该厂日盈利额

(2)为了获得最大盈利,该厂的日产量应定为多少件?
正确答案
解析
解析已在路上飞奔,马上就到!