- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知复数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知点P是双曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.如下图,给定两个平面向量




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知数列




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.某程序框图如图所示,则输出的结果是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.某地为了调查职业满意度,决定用分层抽样的方法从公务员、教师、自由职业者三个群体的相关人员中抽取若干人组成调查小组,相关数据见下表:
则调查小组的总人数为( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.一个球与正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.若变量


正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
16.以下正确命题的序号为__________
①命题“存在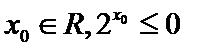

②函数
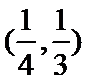
③若函数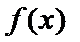
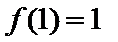
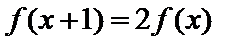
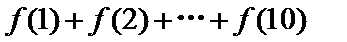
④函数
正确答案
②③
解析
解析已在路上飞奔,马上就到!
知识点
13.已知正数数列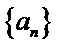
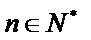
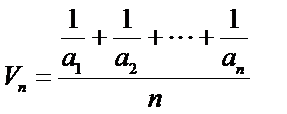
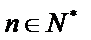
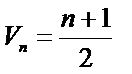
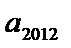
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.一个空间几何体的三视图如右图所示,其中主视图和侧视图都是半径为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF。
正确答案
(Ⅰ)在Rt△ABC中,AB=1,
∠BAC=60°,∴BC=
在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2
∴SABCD=

则V=
(Ⅱ)∵PA=CA,F为PC的中点,
∴AF⊥PC.
∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC.
∵AF∩EF=F,∴PC⊥平面AEF.
解析
解析已在路上飞奔,马上就到!
知识点
17.阅读下面材料:
根据两角和与差的正弦公式,有


由①+② 得
令
代入③得 
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:

(Ⅱ)若



(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
正确答案
解法一:(Ⅰ)证明:因为

①-② 得
令

代入③得
(Ⅱ)由二倍角公式,

所以
设

由正弦定理可得
根据勾股定理的逆定理知
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的结论和二倍角公式,

因为A,B,C为

所以
又因为

所以
从而
又


所以
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆



(Ⅰ)求椭圆
(Ⅱ)垂直于坐标轴的直线






正确答案
(Ⅰ)
(Ⅱ)证明:设

此时0到AB的距离为
同理可求得
综上所述,圆D的半径为定值
解析
解析已在路上飞奔,马上就到!
知识点
21.已知函数f(x)=ax+lnx,其中a为常数,设e为自然对数的底数.
(1)当a=-1时,求f(x)的最大值;
(2)若f(x)在区间(0,e]上的最大值为-3,求a的值;
(3)当a=-1时,试推断方程

正确答案
(1)当a=-1时,f(x)=-x+lnx,f′(x)=-1+
当0<x<1时,f′(x)>0;当x>1时,f′(x)<0.
∴f(x)在(0,1)上是增函数,在(1,+∞)上是减函数

(2) ∵f′(x)=a+

① 若a≥
∴
② 若a<

由f(x)<0

从而f(x)在

∴

令-1+ln

∴





(3)由(Ⅰ)知当a=-1时
∴|f(x)|≥1
又令g(x)=

当0<x<e时,g′(x)>0,g(x) 在(0,e)单调递增;
当x>e时,g′(x)<0,g(x) 在(e,+∞)单调递减
∴

∴|f(x)|>g(x),即|f(x)|>
∴方程|f(x)|=
解析
解析已在路上飞奔,马上就到!
知识点
请考生在第22、23、24三题中任选择一题作答,如果多做,则按所做的第一题记分
22.选修4-1:几何证明选讲
如图,圆






求证:
(Ⅰ)PA·PD=PE·PC;
(Ⅱ)AD=AE。
23.选修4—4:坐标系与参数方程
在极坐标系中,曲线




(Ⅰ)以极点为原点,极轴为x轴的正半轴,取与极坐标相同单位长度,建立平面直角坐标系,写出曲线L和直线
(Ⅱ)求|BC|的长。
24.选修4—5:不等式选讲
已知关于x的不等式

(Ⅰ)当a=4时,求不等式的解集;
(Ⅱ)若不等式有解,求实数a的取值范围。
正确答案
22.(Ⅰ)


又


由①,②得


设

∵

∴
∴

由(Ⅰ)知




又∵

又
∴
23.(Ⅰ)由题意得,点
曲线L的普通方程为:
直线l的普通方程为:
(Ⅱ)设B(


由韦达定理得
由弦长公式得
24.(Ⅰ)当








∴不等式的解集为
(Ⅱ)∵设
故

解析
解析已在路上飞奔,马上就到!
知识点
19.某大学为调查来自南方和北方的同龄大学生的身高差异,从2011级的年龄在1819岁之间的大学生中随机抽取了来自南方和北方的大学生各10名,测量他们的身高,量出的身高如下:(单位:cm)
南方:158,170,166,169,180,175,171,176,162,163;
北方:183,173,169,163,179,171,157,175,178,166;
(1)根据抽测结果,画出茎叶图,并根据你画的茎叶图,对来自南方和北方的大学生的身高作比较,写出两个统计结论;
(2)若将样本频率视为总体的概率,现从来自南方的身高不低于170的大学生中随机抽取3名同学,求其中恰有两名同学的身高低于175的概率。
正确答案
(1)茎叶图如下:
统计结论:(给出下列四个供参考,考生只要答对其中两个即给满分,给出其他合进的答案也给分)
北方大学生的平均身高大于南方大学生的平均身高;
南方大学生的身高比北方大学的身高更整齐;
南方大学生的身高的中位数为169.5cm,北方大学生的身高的中位数为172cm;
南方大学生的高度基本上是对称的,而且大多数集中在均值附近,北方大学生的高度分布较为分散.
(2)南方大学生身高不低于170的有170, 180,175,171,176,从中抽取3个相当于从中抽取2个,共有10种抽法,低于175的只有 2个,所以共有3种,概率为
解析
解析已在路上飞奔,马上就到!