文科数学南通市2011年高三试卷

精品

填空题
简答题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、简答题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题5分，共70分。把答案填写在题中横线上。

题型：填空题

分值: 5分

2．已知，则＝（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

任意角的概念

题型：填空题

分值: 5分

8．已知等比数列的前项和为，若，则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

1．复数的虚部为（）

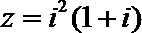
正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

虚数单位i及其性质

题型：填空题

分值: 5分

3．若曲线在点处的切线平行于直线，则点的坐标为（）

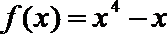
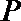
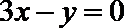
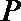
正确答案

（1，0）

解析

解析已在路上飞奔，马上就到！

知识点

定义法求轨迹方程

题型：填空题

分值: 5分

4．如图所示，墙上挂有一边长为的正方形木板，它的四个角的空白部分都是以正方形的顶点为圆心，半径为的圆弧，某人向此板投镖，假设每次都能击中木板，且击中木板上每个点的可能性都一样，则他击中阴影部分的概率是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：填空题

分值: 5分

5．设，若，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质

题型：填空题

分值: 5分

6．若椭圆的左、右焦点分别为，线段被抛物线的焦点分成5﹕3的两段，则此椭圆的离心率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程

题型：填空题

分值: 5分

7．下面伪代码的输出结果为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

流程图的概念

题型：填空题

分值: 5分

9．将一枚骰子抛掷两次，若先后出现的点数分别为，则方程有实根的概率为（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系

题型：填空题

分值: 5分

10．已知函数，则=（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：填空题

分值: 5分

11．将正奇数下表其中第行第个数表，例如，若，则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

12．已知点为的外心，且,则（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：填空题

分值: 5分

13．数列中，，且（，），则这个数列的通项公式（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：填空题

分值: 5分

14．设函数，记，若函数至少存在一个零点，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

简答题（综合题）本大题共90分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

15．已知向量。

（1）求的最小正周期和单调增区间；

（2）如果中，满足，求角的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 15分

17．某网球中心欲建连成片的网球场数块，用128万元购买土地10000平方米，该中心每块球场的建设面积为1000平方米，球场的总建筑面积的每平方米的平均建设费用与球场数有关，当该中心建球场块时，每平方米的平均建设费用(单位：元)可近似地用来刻画。为了使该球场每平方米的综合费用最省(综合费用是建设费用与购地费用之和)，该网球中心应建几个球场?

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素

题型：简答题

分值: 15分

18．已知直线的方程为，且直线与轴交于点，圆与轴交于两点。

（1）过点的直线交圆于两点，且圆孤恰为圆周的，求直线的方程；

（2）求以为准线，中心在原点，且与圆恰有两个公共点的椭圆方程；

（3）过点作直线与圆相切于点,设（2）中椭圆的两个焦点分别为,求三角形面积。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线的倾斜角与斜率

题型：简答题

分值: 14分

16．直棱柱中，底面是直角梯形，,‍。

（Ⅰ）求证：⊥平面；

（Ⅱ）在上是否存一点，使得与平面与平面都平行？证明你的结论。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征

题型：简答题

分值: 16分

19．已知数列中，且点在直线上。

（1）求数列的通项公式；

（2）若函数，求函数的最小值；

（3）设表示数列的前项和．问：是否存在关于的整式，使得对于一切不小于2的自然数恒成立？若存在，写出的解析式，并加以证明；若不存在，试说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项

题型：简答题

分值: 16分

20．已知函数定义域为(),设。

（Ⅰ）试确定的取值范围,使得函数在上为单调函数；

（Ⅱ）求证：；

（Ⅲ）求证：对于任意的,总存在,满足,并确定这样的的个数。

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷