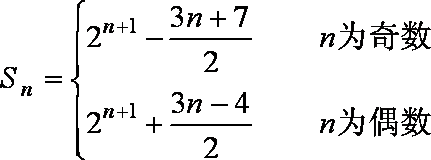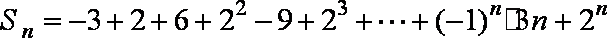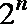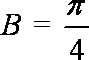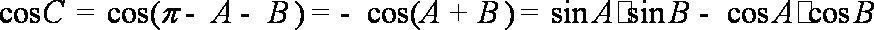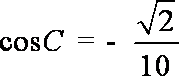- 真题试卷
- 模拟试卷
- 预测试卷
2.在

正确答案
解析
因为


即





知识点
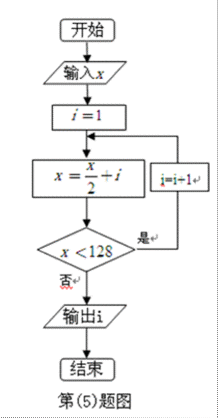
5.如下流程图所示的程序,如果输出i=3,则x的最小值为( )
正确答案
解析
运行流程图,由于输出i=3.所以i=1时,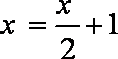





知识点
7.已知


正确答案
解析
因为









知识点
4.某几何体的三视图如下图所示,则该几何体的表面积为( )
正确答案
解析
由三视图可知几何体为下部是底面半径为3,高为6的圆柱,上部是侧棱长为5,底面边长为





知识点
3.下列关于不等式的说法正确的是( )
正确答案
解析
根据基本不等式成立的条件是“一正二定三相等”可知A不正确,因为a、b不一定是正实数;C中一元二次方程的根是1+a和1-a,但是当



知识点
6.已知
正确答案
解析
由于所求的是展开式中所以项的系数和,所以令x=1即可.当x=1时,

知识点
8.平面上画了一


正确答案
解析
由于平行线相距



知识点
1.已知集合

正确答案
解析
因为


知识点
9.在平面直角坐标系xoy中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,已知直线l的极坐标方程为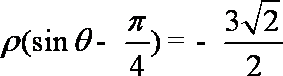
正确答案

解析
由题意可知,直线l: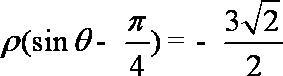
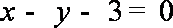
知识点
10.与圆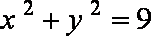
正确答案
解析
设所求圆的圆心C坐标为(x,y),则圆的半径为|x|,又与圆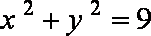
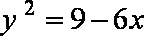
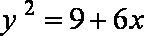

知识点
11.已知向量



正确答案
3
解析
因为







知识点
12.已知数列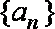
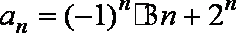
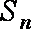
正确答案
解析
因为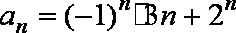
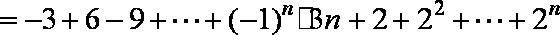
当n为奇数时,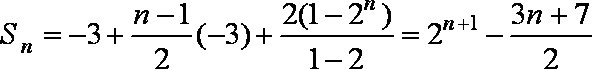
当n为偶数时,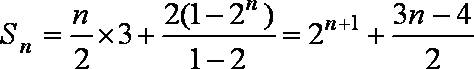
知识点
14.观察下列等式:
(1)若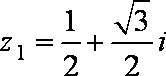


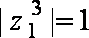

(2)若
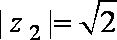

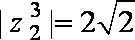

依据你发现的规律,若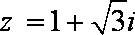

正确答案
解析
由(1)可知模长为1的复数的任何次方的模还是1,由(2)可知任何复数都可以化为一个非负实数乘以一个对应的模长为1的复数,结合(1)(2),
可知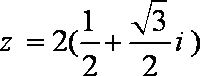
知识点
13.若

正确答案
2014
解析
x>0时,因为



知识点
15.已知A、B、C是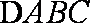
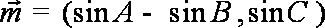
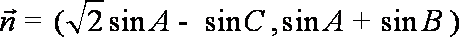
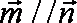
(1)求角B的大小;
(2)若
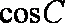
正确答案
见解析。
解析
(1)∵向量
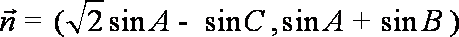
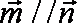
所以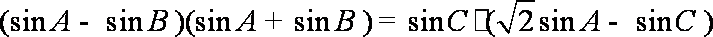
由正弦定理可得:
再由余弦定理可得: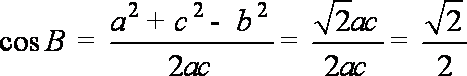
(2)由(1)得
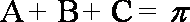
所以

所以
知识点
20.已知如图,在平面直角坐标系xoy中,点B

(1)求出椭圆C的方程;
(2)当直线PA平分FB时,求k的值;
(3)当k=2时,求点P到直线AC的距离;
(4)是否存在正实数k使
正确答案
见解析。
解析
(1)因为椭圆C的长轴长为4,点B



(2)由题意可知F为


(3)当k=2时,直线l的方程为

解得P点为



(4)存在正实数k使

可得




所以
因为k(k>0),当且仅当

知识点
16.已知如图,四边形ABCD是直角梯形,AD//BC,CD⊥AD,PA⊥平面ABCD,
(1)求证:BD//平面AEF;
(2)求直线CE与平面PAB所成角的正切值;
(3)求平面AEF与平面ABCD所成二面角的余弦值。
正确答案
见解析。
解析
(1)证明:连接BD,因为E、F分别是PB、PD的中点.在

(2)因为ABCD是直角梯形,CD⊥AD,





故
(3)分别取AB、AD的中点H、G,连接EH、HG、FG,由(Ⅱ)可知,








知识点
19.设函数
(1)若曲线


(2)讨论
(3)讨论方程
正确答案
见解析。
解析
(1)因为曲线




所以
(2)因为
所以当




当






在
(3)因为方程

令


解得x=-1(舍),x=1,所以

所以
当b-1>0即b>1时,方程
当b=1时,方程
当b<0时,方程
知识点
17.某电视台一档娱乐选秀节目2013-2014年度更新了新规则,制定了由一轮晋级二轮的规则如下:每名选手准备三个节目,按顺序表演.第一个节目有专业评委全票通过,则直接晋级第二轮,否则表演第二个和第三个节目;第二个节目由专业评委投票是否通过,第三个节目由现场观众投票是否通过.若第二个节目获得专业评委三分之二及以上票数通过且第三个节目得到现场观众三分之二及以上票数以上,则晋级第二轮;若第二个节目没有获得专业评委三分之二票数通过,但第三个节目获得现场观众全票通过,也同样晋级到第二轮,否则被淘汰.某位选手估计自己三个节目的通过概率如下表:
若晋级,后面的节目不需要再表演,也不考虑中途自己退出比赛的情况.
(1)求该选手晋级表演节目数
(2)求该选手晋级的概率。
正确答案
见解析。
解析
(1)由题意可知随机变量

表演节目数
(2)该选手晋级可以是第一个节目专业评委全票通过;也可以是第二个节目获得专业评委三分之二及以上票数通过且第三个节目得到现场观众三分之二及以上票数以上;或者是第二个节目没有获得专业评委三分之二票数通过,但第三个节目获得现场观众全票通过,设该选手晋级的事件为A,
则
知识点
18.正项数列

(1)求出

(2)若数列


(3)若数列


正确答案
见解析。
解析
(1)
所以


(2)利用数学归纳法证明:因为

假设当n=k时成立,即
所以当n=k+1时,

所以对任意正整数n,
(3)因为


所以