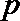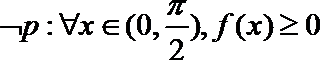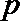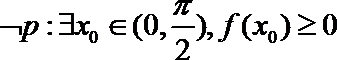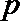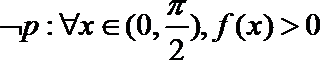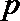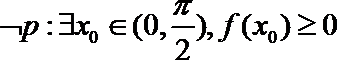- 真题试卷
- 模拟试卷
- 预测试卷
3.函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.已知定义在R上的奇函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.定义运算



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.若曲线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.如下面图所示,半径为2的

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知曲线方程f(x)=sin2x+2ax(a∈R),若对任意实数m,直线l:x+y+m=0都不是曲线y=f(x)的切线,则a的取值范围是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.已知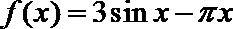
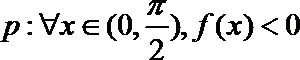
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.定义域为















正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(Ⅰ)若


(Ⅱ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
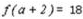

(I)求a的值;
(II)若函数g(x)在区间[0,1]上是单调递减函数,求实数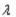
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 
(1)判断
(2)若

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 函数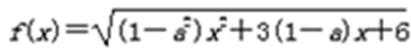
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知函数
(1)若函数



(2)若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 统计表明:某种型号的汽车在匀速行驶中每小时的耗油量



(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13. 函数y=-(x-3)|x|的递减区间是__________.
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.若函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14. 若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数
正确答案
解析
解析已在路上飞奔,马上就到!