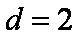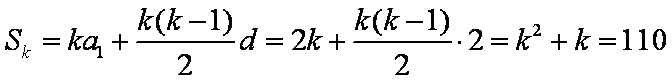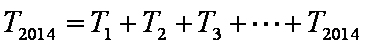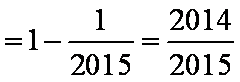- 真题试卷
- 模拟试卷
- 预测试卷
4.已知




正确答案
解析
结合图像,由奇函数性质易得答案。选B
知识点
5.设随机变量

正确答案
解析
因为
所以P(2<X<4)= 
知识点
6.在




正确答案
解析

知识点
9.在△ABC中,若|





正确答案
解析
若|



则

即有
E,F为BC边的三等分点,
则






=(



=




故选B.
知识点
2.已知集合

正确答案
解析
本题考查不等式的解集及其集合间的运算。根据题意知


知识点
8.已知函数

正确答案
解析
∵f(x)=

∴f(﹣x)=1﹣
∴f(x)+f(﹣x)=2;
∵f(a)=
∴f(﹣a)=2﹣f(a)=2﹣

故选C.
知识点
1.设

正确答案
解析
本题考查复数的运算知识,由
知识点
3.“

正确答案
解析
∵a<-4,f(x)=ax+3,
∴f(0)=3>0,f(1)=a+3<(-4)+3=-1<0,f(0)•f(1)<0
∴函数f(x)=ax+3在区间[0,1]上存在零点x0.
∴a<-4”是“函数f(x)=ax+3在区间[-1,1]上存在零点x0”的充分条件;
反之,若函数f(x)=ax+3在区间[-1,1]上存在零点,则f(-1)•f(1)≤0,即(-a+3)(a+3)≤0解得a≤−3或a≥3,
∴a<-4不是“函数f(x)=ax+3在区间[-1,2]上存在零点的必要条件.故选A.
知识点
7.若曲线
正确答案
解析
∵
∴f'(x)=
∴在点(a,f(a))处的切线斜率k=f'(a)=
且f(a)=
∴切线方程为y﹣

令x=0,则y=
令y=0,则x=3a,即切线与坐标轴的交点坐标为(0,
∴三角形的面积为
即
知识点
10.已知抛物线


正确答案
解析
抛物线的焦点为











知识点
11.定义域为R的偶函数f(x)满足∀x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18.若函数y=f(x)﹣loga(x+1)至少有三个零点,则a的取值范围是( )
正确答案
解析
∵f(x+2)=f(x)﹣f(1),且f(x)是定义域
为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
f(﹣1)=f(1),
即 f(1)=0 则有,f(x+2)=f(x),
∴f(x)是周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2,
函数的图象为开口向下.顶点为(3,0)的抛物线.
∵函数y=f(x)﹣loga(|x|+1)在(0,+∞)上
至少有三个零点,
令g(x)=loga(|x|+1),则f(x)的图象和g(x)的图象至少有3个交点.
∵f(x)≤0,∴g(x)≤0,可得a<1.
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上至少有三个零点,
则有g(2)>f(2),可得 loga(2+1)>f(2)=﹣2,
∴loga3>﹣2,∴3<


又a>0,∴0<a<
故选:B.
知识点
12.设双曲线





正确答案
解析
双曲线的渐近线为:y=±



∵


∴λ+μ=1,λ﹣μ=


又由λμ=




∴e=
故选C.
知识点
13.点



正确答案
解析
略。
知识点
16.如图,在△ABC中,已知B=,AC=4,D为BC边上一点.若AB=AD,则△ADC的周长的最大值为________.
正确答案
8+4
解析
∵AB=AD,B=


∴△ADC的周长为
知识点
14.下图茎叶图是甲.乙两人在5次综合测评中成绩,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为()
正确答案
解析
由图可知,甲的5次成绩分别是88.89.90.91.92,易知甲的平均分为90.乙的成绩分别是83.83.87.99,其中被污损的那次成绩为90到99中的某一个.设被污损的那次成绩为





知识点
15.已知数列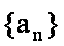
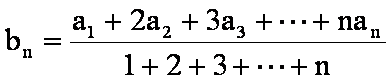
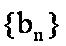
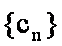
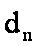
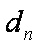
正确答案
解析
由等差数列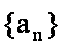
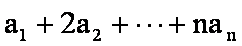
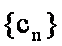
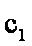
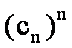
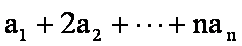
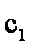
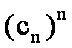

知识点
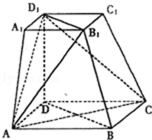
20.如图,在四棱台ABCD﹣A1B1C1D1中,下底ABCD是边长为2的正方形,上底A1B1C1D1是边长为1的正方形,侧棱DD1⊥平面ABCD,DD1=2.
(1)求证:B1B∥平面D1AC;
(2)求证:平面D1AC⊥平面B1BDD1.
正确答案
见解析。
解析
(1)证明:设AC∩BD=E,连接D1E,
∵平面ABCD∥平面A1B1C1D1.
∴B1D1∥BE,∵B1D1=BE=
∴四边形B1D1EB是平行四边形,
所以B1B∥D1E.
又因为B1B⊄平面D1AC,D1E⊂平面D1AC,
所以B1B∥平面D1AC
(2)证明:侧棱DD1⊥平面ABCD,AC⊂平面ABCD,
∴AC⊥DD1.
∵下底ABCD是正方形,AC⊥BD.
∵DD1与DB是平面B1BDD1内的两条相交直线,
∴AC⊥平面B1BDD1
∵AC⊂平面D1AC,∴平面D1AC⊥平面B1BDD1.
知识点
19.某班50名学生在一次数学测试中,成绩全部介于50与100之间,将测试结果按如下方式分成五组:第一组[50,60),第二组[60,70),…,第五组[90,100].如图所示是按上述分组方法得到的频率分布直方图.
(1)若成绩大于或等于60且小于80,认为合格,求该班在这次数学测试中成绩合格的人数;
(2)从测试成绩在[50,60)∪[90,100]内的所有学生中随机抽取两名同学,设其测试成绩分别为m.n,求事件“|m﹣n|>10”概率.
正确答案
见解析。
解析
(1)由直方图知,成绩在[60,80)内的人数为:50×10×(0.18+0.040)=29.
所以该班在这次数学测试中成绩合格的有29人.
(2)由直方图知,成绩在[50,60)内的人数为:50×10×0.004=2,
设成绩为x.y
成绩在[90,100]的人数为50×10×0.006=3,设成绩为a.b.c,
若m,n∈[50,60)时,只有xy一种情况,
若m,n∈[90,100]时,有ab,bc,ac三种情况,
若m,n分别在[50,60)和[90,100]内时,有
共有6种情况,所以基本事件总数为10种,
事件“|m﹣n|>10”所包含的基本事件个数有6种
∴
知识点
18.设等差数列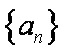
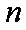
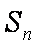
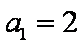
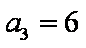
(1)求数列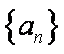
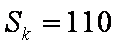
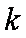
(3)设数列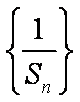
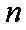
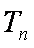
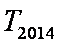
正确答案
见解析。
解析
(1)设等差数列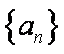
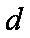
∵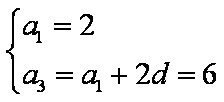
∴
数列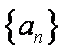
(2)方法一:∵
解得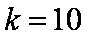
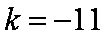
方法二:∵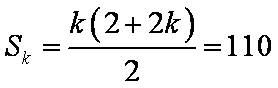
解得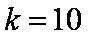
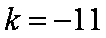
(3)∵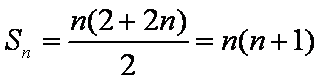

∴
知识点
17.已知函数

(1)求函数
(2)已知







正确答案
见解析。
解析
(1)

由




(2)∵

∵


即
由余弦定理

即
∴
知识点
21.已知椭圆



(1)求椭圆
(2)如图,过右焦点












求证: 
正确答案
见解析。
解析
(1)由条件
故所求椭圆方程为
(2)设过点


由
因为点


设点

因为直线

直线
令


所以点

直线
所以