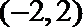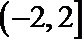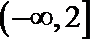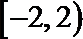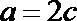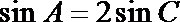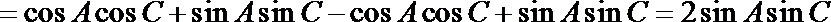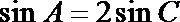- 真题试卷
- 模拟试卷
- 预测试卷
1.设集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若f (x)是偶函数,且当
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在锐角三角形中,a、b、c分别是内角A、B、C的对边,设B=2A,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6..函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.设函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下列函数中,既是偶函数,又在区间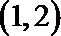
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.O是


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.不等式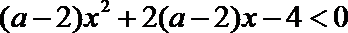
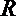
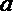
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.等差数列



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.曲线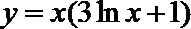
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.在等差数列{an}中,已知a1=20,前n项和为Sn,且S10=S15,求当n=_____ 时,Sn取得最大值
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20. 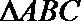
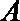
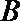
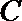

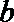

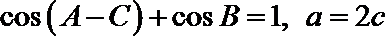
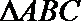
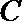
正确答案
解:由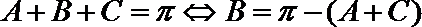
可得
所以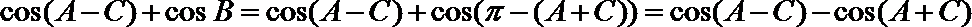
故由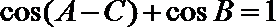
可得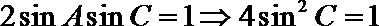
而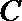
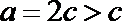
故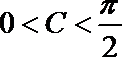
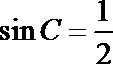

解析
解析已在路上飞奔,马上就到!
知识点
17.设


正确答案
解:1:当



2:当


综上所述,实数m的取值范围是:
解析
解析已在路上飞奔,马上就到!
知识点
18. 已知函数
(1)若

(2)若



正确答案
(1)由

由

因为




(2)当x[1,2]时,2-x[0,1],
因此
由单调性可得
因为

解析
解析已在路上飞奔,马上就到!
知识点
22. 已知
(1)求函数

(2)对一切

(3)证明:对一切


正确答案
(1)


当


①0<t<t+2<

②0<t<


③






(2)

设





因为对一切

(3)问题等价于证明

由(1)可知

当且仅当



当且仅当



解析
解析已在路上飞奔,马上就到!
知识点
19.已知向量
(1)当向量


(2)求函数

正确答案
(1))


(2)




得
解析
解析已在路上飞奔,马上就到!
知识点
21. 已知数列

(1)求证:数列

(2)设数列



正确答案
(1)当n=1时,

当n

即:




所以

(2)




当n=5时
解析
解析已在路上飞奔,马上就到!