• 职业资格类
  • 建筑类
  • 学历类
  • 财会类
  • 医药类
  • 全部考试
  • 教师招募
职业资格类
建筑类
学历类
财会类
计算机类
公务员
医药类
文科数学 兰州市2011年高三试卷
精品
|
立即下载

文科数学 热门试卷

X 查看更多试卷
试卷目录
1、单选题
1
2
3
4
5
6
7
8
9
10
2、填空题
11
12
13
14
15
3、简答题
16
17
18
19
20
21
  • 真题试卷
  • 模拟试卷
  • 预测试卷
查看更多 >
单选题 本大题共10小题，每小题5分，共50分。在每小题给出的4个选项中，有且只有一项是符合题目要求。
1
题型： 单选题
|
分值: 5分

3.一篮球运动员投篮命中的概率是，他连续投篮次，则恰有次命中的概率是（    ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系
1
题型： 单选题
|
分值: 5分

1.已知向量与向量，则向量与的夹角是（    ）

A

B

C

D

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征
1
题型： 单选题
|
分值: 5分

5.设，，若是的必要而不充分条件，则实数的取值范围是  （     ）

A

B

C∪

D∪

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

变化的快慢与变化率
1
题型： 单选题
|
分值: 5分

6.函数是   （     ）

A周期为的偶函数

B周期为的非奇非偶函数

C周期为的偶函数

D周期为的非奇非偶函数

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型： 单选题
|
分值: 5分

8.已知函数在区间上的最小值是，则的取值范围为（    ）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型： 单选题
|
分值: 5分

2.若，则下列不等式中不一定成立的是 （    ）

A

B 

C

D∣∣>

正确答案

B

解析

解析已在路上飞奔，马上就到！

知识点

不等式的性质
1
题型： 单选题
|
分值: 5分

4.已知集合，，则

（     ）

A

B

C

D

正确答案

D

解析

解析已在路上飞奔，马上就到！

知识点

集合的含义
1
题型： 单选题
|
分值: 5分

7.已知函数是定义在上的单调函数，且对任意的正数，都有，若数列的前项和为，且满足，则   （    ）

A

B

C

D

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型： 单选题
|
分值: 5分

9.已知函数，其中，则使得在

上有解的概率为   （    ）

A

B

C

D

正确答案

A

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程
1
题型： 单选题
|
分值: 5分

10.设双曲线的右顶点为，为双曲线上的一个动点（不是顶点），从点引双曲线的两条渐近线的平行线，与直线分别交于两点，其中为坐标原点，则与的大小关系为 （    ）

A

B

C

D不确定

正确答案

C

解析

解析已在路上飞奔，马上就到！

知识点

双曲线的定义及标准方程
填空题 本大题共5小题，每小题5分，共25分。把答案填写在题中横线上。
1
题型：填空题
|
分值: 5分

13.将抛物线按向量平移后所得抛物线的焦点坐标为_______．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

抛物线的定义及应用
1
题型：填空题
|
分值: 5分

14.若等差数列的前项和为，且，，则 _______．

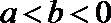
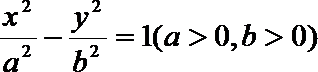
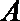
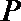
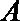
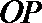
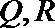
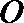
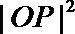
正确答案

17

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项
1
题型：填空题
|
分值: 5分

12.如图，在中，为BC上异于B、C的任一点，为的中点，若，则 ________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征
1
题型：填空题
|
分值: 5分

11.为了了解我校今年准备报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率分布直方图（如图），已知图中从左到右的前个小组的频率之比为，第小组的频数为，则抽取的学生人数是_______．

正确答案

48

解析

解析已在路上飞奔，马上就到！

知识点

随机事件的关系
1
题型：填空题
|
分值: 5分

15.给出定义：若 (其中为整数)，则叫做离实数最近的整数，记作，即. 在此基础上给出下列关于函数的四个命题：
①的定义域是，值域是；

②点是的图像的对称中心；

③函数的最小正周期为1；

④ 函数在上是增函数；

则其中真命题是______．

正确答案

①③

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
简答题（综合题） 本大题共75分。简答应写出文字说明、证明过程或演算步骤。
1
题型：简答题
|
分值: 12分

18.若关于的实系数方程有两个根，一个根在区间内，另一根在区间内，记点对应的区域为

（1）设，求的取值范围；

（2）过点的一束光线，射到轴被反射后经过区域，求反射光线所在直线经过区域内的整点（即横纵坐标为整数的点）时直线的方程。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

空间几何体的结构特征
1
题型：简答题
|
分值: 12分

19.已知函数的反函数为，定义：若对给定的实数，函数与互为反函数，则称满足“和性质”。

（1）判断函数是否满足“1和性质”，并说明理由；

（2）若，其中满足“2和性质”，则是否存在实数a，使得对任意的恒成立？若存在，求出的范围；若不存在，请说明理由。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型：简答题
|
分值: 12分

17.已知为坐标原点，向量，点是直线上的一点，且点分有向线段的比为

（1）记函数，，讨论函数的单调性；

（2）若三点共线，求的值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的概念及其构成要素
1
题型：简答题
|
分值: 14分

21.已知椭圆的左、右焦点分别为，若以为圆心，为半径作圆，过椭圆上一点作此圆的切线，切点为，且的最小值不小于

（1）证明：椭圆上的点到点的最短距离为；

（2）求椭圆的离心率的取值范围；

（3）设椭圆的短半轴长为，圆与轴的右交点为，过点作斜率为的直线与椭圆相交于两点，若，求直线被圆截得的弦长的最大值。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

椭圆的定义及标准方程
1
题型：简答题
|
分值: 13分

20.已知曲线，从上的点作轴的垂线，交于点，再从点作轴的垂线，交于点，设

（1）求数列的通项公式；

（2）记，数列的前项和为，试比较与的大小

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

由数列的前几项求通项
1
题型：简答题
|
分值: 12分

16.已知等比数列中，，分别为的三内角的对边，且．

（1）求数列的公比；

（2）设集合，且，求数列的通项公式．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

点击 “立即下载”

即可下载本试卷，含解析哦

知道啦