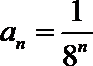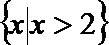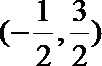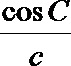- 真题试卷
- 模拟试卷
- 预测试卷
7.集合
正确答案
0.6
解析
解析已在路上飞奔,马上就到!
知识点
10.试在无穷等比数列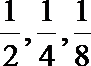

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.若sin


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.在数列




正确答案
20
解析
解析已在路上飞奔,马上就到!
知识点
4.已知函数f(x)的图象与函数
正确答案
2
解析
解析已在路上飞奔,马上就到!
知识点
8.在△ABC中三边之比a:b:c=2:3:
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合A=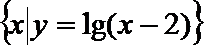
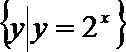

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.某工程由下列工序组成,则工程总时数为( )天。
正确答案
略
解析
解析已在路上飞奔,马上就到!
知识点
11.在R上定义运算△:x△y=x(1 -y) 若不等式(x-a)△(x+a)<1,对任意实数x恒成立,则实数a的取值范围是( )。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知数列


图所示.记

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.若复数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.函数y=cos 2x的图象的一个对称中心是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.函数y=
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.某人骑自行车沿直线匀速旅行,先前进了





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某自来水厂的蓄水池存有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,


(1)从供水开始到第几小时时,蓄水池中的存水量最少?最少水量是多少吨?
(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象。
正确答案
(1)设


令

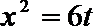

∴当


(2)依题意





解析
解析已在路上飞奔,马上就到!
知识点
21.设有

(1)求数列{xn}的通项公式;
(2)若
(3)是否存在最小整数m,使得对任意n∈N*,有
正确答案
(1)因方程f(x)=x有唯一解,可求a=

数列{


故

所以数列{xn}的通项公式为
(2)将xn代入an可求得an=2n-1,所以
(3)
即要
解析
解析已在路上飞奔,马上就到!
知识点
18.已知向量


(1)求函数f(x)的最小正周期。
(2)x
正确答案
f(x)=




(1)T=

(2)f(x)=2sin(2x+











解析
解析已在路上飞奔,马上就到!
知识点
17.设为虚数,且满足

正确答案
设
则
由已知得

∴ 

解析
解析已在路上飞奔,马上就到!
知识点
22.设函数f(x)=ax
(1)若f(-1)=0且对任意实数x均有f(x)
(2)在(1)的条件下,当x
正确答案
(1)
由f(x)
知△=b


∴a=1从而f(x)=x
∴F(x)=
(2)由(1)可知f(x)=x
∴g(x)=f(x)-kx=x
由于g(x)在
知-

得k

解析
解析已在路上飞奔,马上就到!
知识点
19.在不等边△ABC中,设A.B.C所对的边分别为a,b,c,已知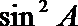
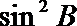
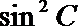
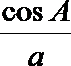
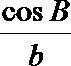
(1)试根据下列选项作出判断,并在括号内填上你认为是正确选项的代号( )
A.是等比数列而不是等差数列
B.是等差数列而不是等比数列
C.既是等比数列也是等差数列
D.既非等比数列也非等差数列
(2)证明你的判断
正确答案
(1)B
(2)因为

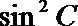
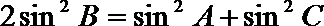
所以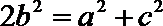
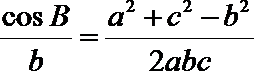

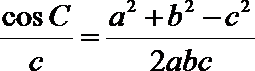
显然
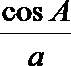
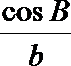
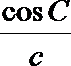
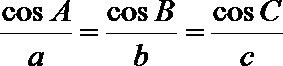

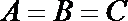
解析
解析已在路上飞奔,马上就到!