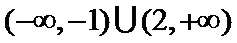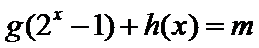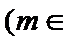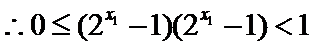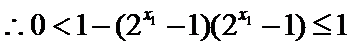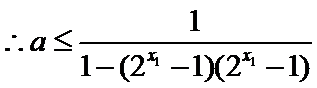- 真题试卷
- 模拟试卷
- 预测试卷
10.某足球队共有11名主力队员和3名替补队员参加一场足球比赛,其中有2名主力和1名替补队员不慎误服违禁药物,依照比赛规定,比赛后必须随机抽取2名队员的尿样化验,则能查到服用违禁药物的主力队员的概率为 ( )。(结果用分数表示)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.方程
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.设




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.已知下列三组条件:
(1)

(2)


(3)






其中

正确答案
(1)(2)
解析
解析已在路上飞奔,马上就到!
知识点
8.函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.在




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.不等式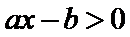
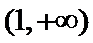
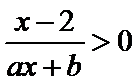
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数
①函数的定义域为
②

③

④

写出满足上述性质的一个函数为
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.如果











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.若





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
13.对


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知
(1)求
(2)求
正确答案

∴
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,圆







(1)求动点

(2)过点







正确答案
(1)设

所以
又P在圆
所以
即
即
轨迹是以

长轴长为4的椭圆
(2)方法一:当直线

设直线

代入椭圆方程得:
△
设
则
由
所以
由(*)、(**)
解得

所以
即所求直线方程为:
解析
解析已在路上飞奔,马上就到!
知识点
23.设数列





(1)若

(2)若

(3)若


正确答案
(1)由题意,得
解
∴

(2)由题意,得
对于正整数,由

根据
当

当

∴

(3)假设存在p和q满足条件,由不等式


∵


即
当



这与上述结论矛盾!
当



∴ 存在p和q,使得
p和q的取值范围分别是
解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数
(1)若

(2)若


正确答案
(1)当


由条件可知 

解得

(2)当
即 



故
解析
解析已在路上飞奔,马上就到!
知识点
22.对定义在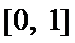
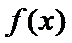
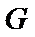
① 对任意的
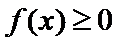
② 当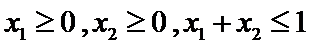
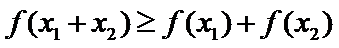
已知函数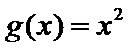
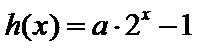
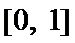
(1)试问函数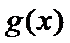
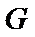
(2)若函数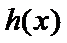
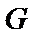
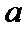
(3)在(2)的条件下
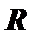
正确答案
(1) 当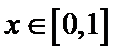
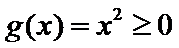
当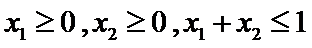
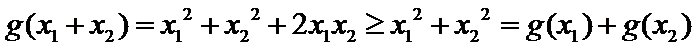
(2)若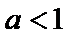
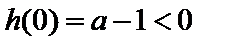
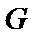
若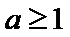
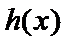
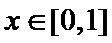
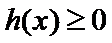
由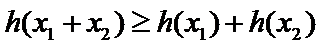
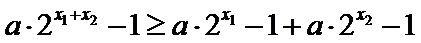
即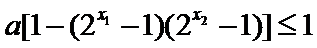
因为
所以 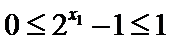
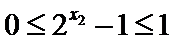

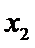
当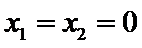
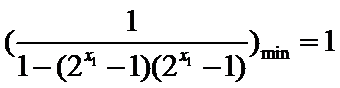
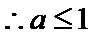
综合上述: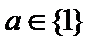
(3)根据(2)知: a=1,方程为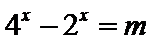
由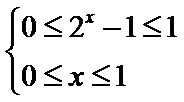
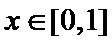
令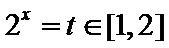
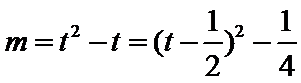
由图形可知:当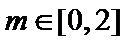
当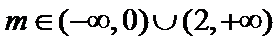
解析
解析已在路上飞奔,马上就到!
知识点
17.设函数








正确答案
解析
解析已在路上飞奔,马上就到!
知识点
18.若



①

②

③


④函数


则以上各命题中正确的个数是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15.集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.函数
正确答案
解析
解析已在路上飞奔,马上就到!