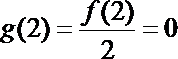- 真题试卷
- 模拟试卷
- 预测试卷
3.设






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.设命题


正确答案
解析
全称命题的否定,要把量词任意改为存在,且否定结论,故非


知识点
5.若函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.定义在R上的偶函数






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.若函数











正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.给定









正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知集合



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.函数





正确答案
解析
由
知
所以
因为

所以点


点

所以

知识点
9.对于函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1.已知集合


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.已知函数



正确答案
解析
令

令
则
所以
知识点
13.已知函数





正确答案
-1
解析
解析已在路上飞奔,马上就到!
知识点
15.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.已知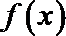
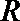
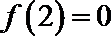
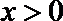
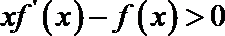
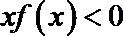
正确答案
解析
显然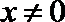
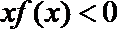
同解.记
则当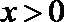
从而可知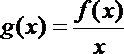

又
画出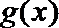
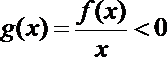
即不等式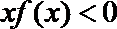
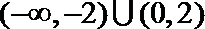
知识点
14.在集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数




(1)求
(2)解不等式
正确答案
解:(1)令x=y=1,
则f(1)=f(1)+f(1),f(1)=0.
(2)由题意知f(x)为(0,+∞)上的减函数,
且
∵f(xy)=f(x)+f(y),x.y∈(0,+∞) 且f
∴f(-x)+f(3-x)≥-2,
可化为f(-x)+ f(3-x)≥-2f
f(-x)+f

f


解得-1≤x<0.
∴不等式的解集为[-1,0).
解析
解析已在路上飞奔,马上就到!
知识点
18.已知函数

(1)若
(2)若f(x)是增函数,求实数
正确答案
解:(1)


极大值
(2)





解析
解析已在路上飞奔,马上就到!
知识点
19.对定义在


① 对任意的

② 当




(1)试问函数

(2)若函数


正确答案
解:(1)当

当

所以函数

(2)
由

即
因为
所以 




当

综合上述:
解析
解析已在路上飞奔,马上就到!
知识点
21.已知

(1)求
(2)设函数


正确答案
解:(1)






(2)由(1)得
所以
所以
于是当



故
不妨设

而
故以
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数

(1)求集合A、B;
(2)若

正确答案
解: (1)A=
B=
(2)由

所以

解析
解析已在路上飞奔,马上就到!
知识点
20.已知函数f(x)=

(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)的单调区间。
正确答案
解:(Ⅰ)f(x)=

由f′(1)=2﹣




即


(Ⅱ)由(Ⅰ)可得f′(x)=
即f′(x)=
由x=e时,f′(e)=0,且x>e,e﹣x>0,ex(1﹣lnx)<0,
故f′(x)<0,同理0<x<e,f′(x)>0,
于是函数的单调增区间为(0,e),减区间为(e,+∞).
解析
解析已在路上飞奔,马上就到!