文科数学浦东新区2012年高三试卷

精品

填空题
简答题
单选题

立即下载

文科数学热门试卷

X 查看更多试卷

试卷目录

1、填空题

2、简答题

3、单选题

真题试卷
模拟试卷
预测试卷

填空题本大题共14小题，每小题4分，共56分。把答案填写在题中横线上。

题型：填空题

分值: 4分

2．若的反函数，则 ________。

正确答案

-1

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：填空题

分值: 4分

3．在二项式的展开式中，含的项的系数为________。

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：填空题

分值: 4分

6．如图是一个正三棱柱零件，面平行于正投影面，则零件的左视图的面积为________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

直线与平面平行的判定与性质

题型：填空题

分值: 4分

11．对于任意，不等式恒成立，则实数的取值范围是________。

正确答案

（-∞，-1）∪（3，+∞）

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

1．已知全集，，，则________。

正确答案

（0，1）

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：填空题

分值: 4分

4．函数的单调递减区间是________。

正确答案

（2，+∞）

解析

解析已在路上飞奔，马上就到！

知识点

导数的加法与减法法则

题型：填空题

分值: 4分

7．已知函数，，则函数的值域为________

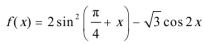
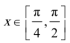
正确答案

[2，3]

解析

解析已在路上飞奔，马上就到！

知识点

诱导公式的作用

题型：填空题

分值: 4分

5．圆锥的侧面展开图为扇形，若其弧长为，半径为，则该圆锥的体积为________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

平行关系的综合应用

题型：填空题

分值: 4分

9．直线上的点到圆上的点的最近距离是 ________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

题型：填空题

分值: 4分

10．在各项均为正数的等比数列中，，则其前3项的和的取值范围是________

正确答案

（-∞，-1]∪[3，+∞]

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：填空题

分值: 4分

13．已知一个袋中装有大小相同的黑球．白球和红球，共有个球，从袋中任意摸出个球，得到黑球的概率是，则从中任意摸出个球，得到的都是黑球的概率为________

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

等差数列的性质及应用

题型：填空题

分值: 4分

14．已知定义在R上的奇函数，满足，且在区间[0，2]上是增函数，若方程f（x）=m（m>0）在区间上有四个不同的根，则 __________

正确答案

-8

解析

解析已在路上飞奔，马上就到！

知识点

求函数y＝Asin(ωx＋φ)的解析式

题型：填空题

分值: 4分

8．设函数，则实数的取值范围是_____________。

正确答案

（-3，1）

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

题型：填空题

分值: 4分

12．已知函数满足对任意都有成立，则a的取值范围是________．

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的图像

简答题（综合题）本大题共74分。简答应写出文字说明、证明过程或演算步骤。

题型：简答题

分值: 14分

20．已知向量，，．

（1）若，求向量．的夹角；

（2）若，函数的最大值为，求实数的值．

正确答案

（1）当时，，

所以因而；

（2），

因为，所以

当时，，即，

当时，，即．

所以．

解析

解析已在路上飞奔，马上就到！

知识点

点与圆的位置关系

题型：简答题

分值: 16分

22．已知函数，．

（1）证明：函数在区间上为增函数，并指出函数在区间上的单调性；

（2）若函数的图像与直线有两个不同的交点，，其中，求的取值范围。

正确答案

（1）证明：任取，，且，

，

．

所以在区间上为增函数．

函数在区间上为减函数．

（2）解：因为函数在区间上为增函数，相应的函数值为，在区间上为减函数，相应的函数值为，由题意函数的图像与直线有两个不同的交点，故有，

易知，分别位于直线的两侧，由，得，故，，又，两点的坐标满足方程，故得，，即，，

故，

当时，，，故，

又，因此；

当时，，，从而；

综上所述，的取值范围为．

解析

解析已在路上飞奔，马上就到！

知识点

利用导数求函数的最值

题型：简答题

分值: 14分

19．如图，在四棱锥中，底面是边长为2的正方形，，，为的中点．

（Ⅰ）求四棱锥的体积；

（Ⅱ）求异面直线OB与MD所成角的大小．

正确答案

（Ⅰ）由已知可求得，正方形的面积，

所以，求棱锥的体积

（Ⅱ）设线段的中点为，连接，

则为异面直线OC与所成的角（或其补角）

由已知，可得，

为直角三角形

，

．

所以，异面直线OC与MD所成角的大小．

解析

解析已在路上飞奔，马上就到！

知识点

导数的乘法与除法法则

题型：简答题

分值: 14分

21．已知圆．

（1）求过点的圆C的切线的方程；

（2）如图，为圆C上一动点，点P在AM上，点N在CM上，且满足求的轨迹方程．

正确答案

（1）由题意知所求的切线斜率存在，设其方程为，即；

由得，解得，

从而所求的切线方程为，

（2）

∴NP为AM的垂直平分线，∴|NA|=|NM|．

∴动点N的轨迹是以点C（－1，0），A（1，0）为焦点的椭圆．

且椭圆长轴长为焦距2c=2．

∴点N的轨迹是方程为

解析

解析已在路上飞奔，马上就到！

知识点

函数的图象与图象变化

题型：简答题

分值: 16分

23．已知：点列（）在直线L：上，为L与轴的交点，

数列为公差为1的等差数列，。

（1）求数列的通项公式；

（2）若（），令；试用解析式写出关于的函数；

（3）若（），是否存在，使得，若存在，求出的值；若不存在，请说明理由。

正确答案

（1）与轴的交点为，；

所以，

即，

因为在上，

所以，

即

（2）若（），

即若（）

（A）当时，

==，

而，

所以

（B）当时，

= =，

而，所以

因此（）

（3）假设存在使得成立。

（A）若为奇数，则为偶数。

所以，，而，

所以，方程无解，此时不存在。

（B）若为偶数，则为奇数。

所以，，

而，所以，解得

由（A）（B）得存在使得成立。

解析

解析已在路上飞奔，马上就到！

知识点

幂函数的概念、解析式、定义域、值域

单选题本大题共4小题，每小题5分，共20分。在每小题给出的4个选项中，有且只有一项是符合题目要求。

题型：单选题

分值: 5分

18．已知函数的图像与函数（且）的图像交于点，如果，那么的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

函数的最值

题型：单选题

分值: 5分

16．设函数的反函数为，对于内的所有的值，下列关系式中一定成立的是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

复合函数的单调性

题型：单选题

分值: 5分

15．设集合，集合，且，则实数的取值范围是（）

正确答案

解析

解析已在路上飞奔，马上就到！

知识点

利用导数证明不等式

题型：单选题

分值: 5分

17．在下列函数中，既是）上的增函数，又是以为最小正周期的偶函数的函数是（）

文科数学 热门试卷

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

正确答案

解析

知识点

文科数学热门试卷