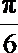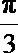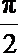- 真题试卷
- 模拟试卷
- 预测试卷
1.抛物线y=4x2的准线方程为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.已知


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.函数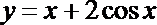
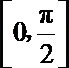

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8.如右图为一个几何体的三视图,尺寸如图所示,则该几何体的体积为 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7.过椭圆
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知平面区域







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
3.已知点

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.已知f(x)=ax2+bx是定义在[a-1,2a]上的偶函数,那么a+b的值是 ( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12.已知椭圆



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.在正方体


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.过双曲线x2-y2=4的左焦点F1有一条弦PQ在左支上,若|PQ|=7,F2是双曲线的右焦点,则△PF2Q的周长是( )
正确答案
22
解析
解析已在路上飞奔,马上就到!
知识点
15.如果圆锥的侧面展开图是半圆,那么这个圆锥的顶角(圆锥轴截面中两条母线的夹角)是( )
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16.第一行:1
第二行:2 3 4
第三行:3 4 5 6 7
第四行:4 5 6 7 8 9 10
… …
从上图观察可得第( )行的各数之和等于
正确答案
1006
解析
解析已在路上飞奔,马上就到!
知识点
13.若曲线



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.如图所示,在棱长为2的正方体




(1)求证:

(2)求证:
(3)求
正确答案
(1)
连结





(2)
(3)
且

∴

=
解析
解析已在路上飞奔,马上就到!
知识点
17.(1)直线经过点P(3,2),且在两坐标轴上的截距相等,求直线方程;
(2)设直线


正确答案
(1)设直线l在x,y轴上的截距均为a,
若a=0,即l过点(0,0)和(3,2),
∴l的方程为y=
若a≠0,则设l的方程为
∵l过点(3,2),∴
∴a=5,∴l的方程为x+y-5=0,
综上可知,直线l的方程为2x-3y=0或x+y-5=0.
(2)圆心(1,2),半径r=2
设圆心到直线的距离为d,则由垂径定理知


解析
解析已在路上飞奔,马上就到!
知识点
18.设






(1)求
(2)求
正确答案
(1)由题意知




∴|


∴S=








∵3≤S≤3
∴3≤3tan


∵



∴
(2)
∵


∴当2




f(
解析
解析已在路上飞奔,马上就到!
知识点
19.已知关于坐标轴对称的椭圆经过两点A(0,2)和B
(1)求椭圆的标准方程
(2)若点P是椭圆上的一点,F1和F2是焦点,且∠F1PF2=30°,求△F1PF2的面积.
正确答案
(1)设经过两点A(0,2),B
mx2+ny2=1,代入A、B得

∴所求椭圆方程为
(2)在椭圆

又∵点P在椭圆上,∴|PF1|+|PF2|=2a=4. ①
由余弦定理知:|PF1|2+|PF2|2-2|PF1||PF2|cos30°=|F1F2|2=(2c)2=12. ②
把①两边平方得|PF1|2+|PF2|2+2|PF1|·|PF2|=16, ③
③-②得(2+
∴|PF1|·|PF2|=4(2-
∴


解析
解析已在路上飞奔,马上就到!
知识点
20.已知数列








(2)若


正确答案
(1)由
相减得:

∵当

∴数列
(2)∵
由题意
设

∴


故
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
(I)当



(II)当
(1)求证:对任意的


(2)若关于




正确答案
(I)当




(II)设
解析
解析已在路上飞奔,马上就到!