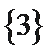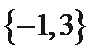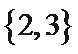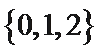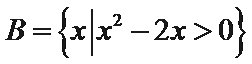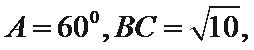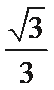- 真题试卷
- 模拟试卷
- 预测试卷
1. 设集合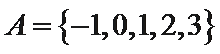
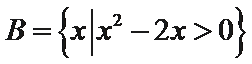
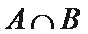
正确答案
解析
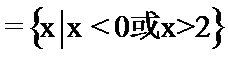
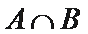
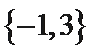
考查方向
解题思路
先计算出集合B,再求交集。
易错点
粗心做错。
知识点
2. 若


正确答案
解析



考查方向
解题思路
先将Z化简算出来再计算其模。
易错点
容易计算失误算错。
知识点
3. 设a,b是实数,则“a>b”是“a2>b2”的( )
正确答案
解析
由a>b不能推出a2>b2,可以举反例,如2>-3,但是4<9,反过来由a2>b2也不能推出a>b,可以举反例,所以选D答案。
考查方向
解题思路
按照步骤来求解。
易错点
判断出错。
知识点
5.执行如图1所示的程序框图,若输入

正确答案
解析



考查方向
解题思路
按步骤来计算即可。
易错点
计算失误。
知识点
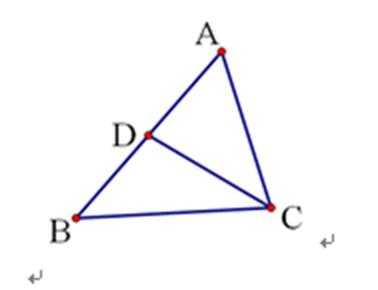
8. 已知






正确答案
解析
根据中点是D,再结合向量加法的平行四边形法则可以得到D也是AP的中点故可以得
考查方向
解题思路
根据中点是D,再结合向量加法的平行四边形法则可以得到D也是AP的中点故可以得到答案。
易错点
不会转化成所学内容。
知识点
9.已知





正确答案
解析



考查方向
解题思路
由最小值为1然后构造方程来计算。
易错点
找不到什么位置取到最小值。
知识点
10.已知中心在原点的椭圆C的右焦点为

正确答案
解析
由题意可知

考查方向
解题思路
根据已知条件构造方程组解答。
易错点
计算错误。
知识点
4.已知
正确答案
解析
由

考查方向
解题思路
直接利用诱导公式化简来做。
易错点
符号弄错。
知识点
6.某三棱锥的三视图如图2所示,则该三棱锥的体积是
正确答案
解析
如图所示,直观图是一个三棱锥,则其体积为
考查方向
解题思路
还原出直观图是一个三棱锥,然后按照体积的公式代入计算即可。
易错点
不会还原直观图。
知识点
7. 在函数①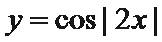
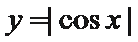
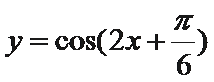
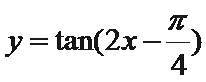
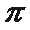
正确答案
解析
.①②③的最小正周期都为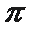
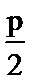
考查方向
解题思路
分别判断。
易错点
判断失误。
知识点
11. 在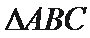
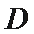
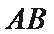
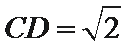
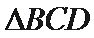
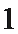
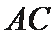
正确答案
解析
如图所示:由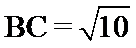
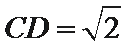
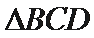
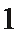
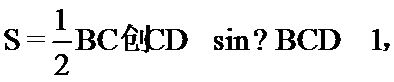
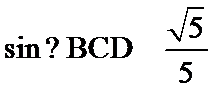
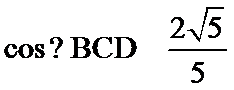
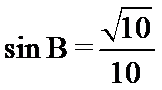
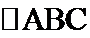
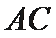
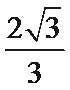
考查方向
解题思路
先画出示意图,再利用定理解决。
易错点
不会灵和使用定理来求解。
知识点
12. 已知函数

正确答案
解析
由已知的解析式可知改函数不是奇函数,所以图像不关于原点对称,排除B,C,当x<0时可知函数的导函数恒小于0 ,也就是单调递减的,所以排除D,所以选A答案。
考查方向
解题思路
根据函数的性质去做。
易错点
不会求解。
知识点
14.若曲线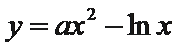
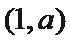
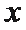
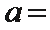
正确答案
解析
由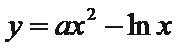
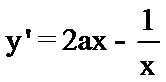
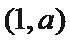
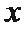
所以满足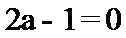

考查方向
解题思路
求导然后由导数为0求解。
易错点
不知道导数的几何意义是什么。
知识点
15.设数列



正确答案
15
解析
数列



+2+4+8=15.
考查方向
解题思路
分别计算出每一项,再相加即可。
易错点
弄错符号。
知识点
16. 




正确答案
32
解析
如下图所示:


考查方向
解题思路
先求出球的半径再计算其表面积。
易错点
不会计算球的半径。
知识点
13.已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则k=_____________.
正确答案
1
解析
已知a与b为两个不共线的单位向量,k为实数,若向量a+b与向量ka-b垂直,则满足
考查方向
解题思路
本题考查采用正确的方法将向量垂直转化为数量积为0的能力。
易错点
向量垂直满足的条件。
知识点
17.(本小题满分12分) 已知数列




(I) 求证:数列
(II) 证明:当

正确答案
(1)见解析;(2)见解析。
解析
试题分析:本题属于等差数列以及等差数列的性质,数列的通项公式和前n项和的关系,(1)根据题意直接利用通项公式和前n项和的关系来证明;(2)利用放缩法来证明。
考查方向
解题思路
本题考查等差数列以及等差数列的性质,数列的通项公式和前n项和的关系,解题步骤如下:(1)根据题意直接利用通项公式和前n项和的关系来证明;(2)利用放缩法来证明。
易错点
找不到通项公式和前n项和的关系。
知识点
20.已知椭圆C:x2+2y2=4.
(II)设O为原点,若点A在直线y=2上,点B在椭圆C上,且OA⊥OB,求线段AB长度的最小值.
正确答案
(1)e==;(2)2。
解析
试题分析:本题属于直线与圆锥曲线的位置关系,题目的难度是逐渐由易到难,
(1)根据已知构造方程组来求解;
(2)先表示出来后利用基本不等式来计算最值。
考查方向
解题思路
本题考查直线与圆锥曲线的位置关系,解题步骤如下:
(1)根据已知构造方程组来求解;
(2)先表示出来后利用基本不等式来计算最值。
易错点
计算容易出错。
知识点
18.截至2014年11月27目,我国机动车驾驶人数量突破3亿大关,年均增长超过两千万.为了解某地区驾驶预考人员的现状,选择A,B,C三个驾校进行调查.参加各驾校科目一预考人数如下:
若用分层抽样的方法从三个驾校随机抽取24人进行分析,他们的成绩如下:
(I)求三个驾校分别应抽多少人?
(II)补全下面的茎叶图,并求样本的众数和极差;
(Ⅲ)在对数据进一步分析时,满足|x-96.5|≤4的预考成绩,称为具有M特性.在样本中随机抽取一人,求此人的预考成绩具有M特性的概率.
正确答案
(1)6,8,10;(2)众数为:92,极差为:99-64=35;(3)P(A)=
解析
试题分析:本题属于分层抽样和古典概型,
(1)利用分层抽样也就是按比例抽样计算即可;
(2)按步骤直接计算;
(3)利用古典概型公式来计算。
考查方向
解题思路
本题考查分层抽样和古典概型,解题步骤如下:
(1)利用分层抽样也就是按比例抽样计算即可;
(2)按步骤直接计算;
(3)利用古典概型公式来计算。
易错点
计算出错。
知识点
19.如图,已知







(I)求证:

(II)求证:

(Ⅲ)求三棱锥
正确答案
(1)见解析;(2)见解析;(3)
解析
试题分析:本题属于立体几何中有关线面平行和线面垂直的证明以及求体积的基本问题,
(1)直接利用线面平行的判定定理来证明;
(2)由线线垂直到线面垂直即线面垂直的判定定理;
(3)换底后直接利用体积公式来求解。
考查方向
解题思路
本题考查立体几何中有关线面平行和线面垂直的证明以及求体积,解题步骤如下:
(1)直接利用线面平行的判定定理来证明;
(2)由线线垂直到线面垂直即线面垂直的判定定理;
(3)换底后直接利用体积公式来求解。
易错点
定理使用条件不全。
知识点
21.已知函数



(I)求a,b的值;
(II)证明:当x>0,且

正确答案
(1)

解析
试题分析:本题属于导数的几何意义及其应用,题目的难度是逐渐由易到难,
(1)根据导数的几何意义,结合已知条件构造方程组即可解出;
(2)利用构造函数之后再求导来证明。
考查方向
解题思路
本题考查导数的性质,解题步骤如下:
(1)根据导数的几何意义,结合已知条件构造方程组即可解出;
(2)利用构造函数之后再求导来证明。
易错点
导函数容易求错。
知识点
22.已知四边形ABCD内接于⊙O,AD:BC=1:2,BA、CD的延长线交于点E,且EF切⊙O于F.
(Ⅰ)求证:EB=2ED;
(Ⅱ)若AB=2,CD=5,求EF的长.
正确答案
(1)见解析;(2)EF=2
解析
试题分析:本题属于几何证明选讲中有关线段成比例的定理,
(1)利用三角形相似对应边成比例即可得证;
(2)切割线定理的使用。
考查方向
解题思路
本题考查几何证明选讲中有关线段成比例的定理,解题步骤如下:
(1)利用三角形相似对应边成比例即可得证;
(2)切割线定理的使用。
易错点
定理不熟。