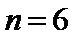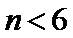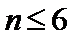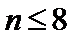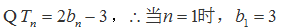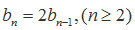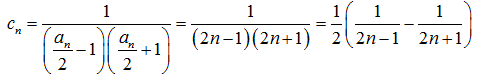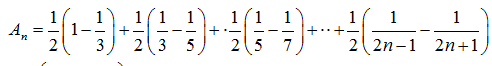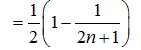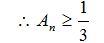- 真题试卷
- 模拟试卷
- 预测试卷
1.设全集

正确答案
解析
由题可得:U={0,1,2,3,4,5,6}。B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
利用图示法,即可得到结果。
B选项不正确,C选项不正确,D选项不正确,所以选A选项。
易错点
本题易在判断补集时发生错误。
知识点
3. 函数
正确答案
解析
由题可知:f(a)f(b)<0,代入计算即可。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
利用零点存在性定理,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在求函数值时发生错误。
知识点
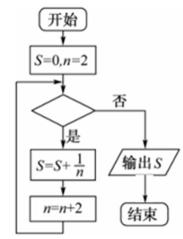
5. 阅读如图所示的程序框图,运行相应的程序.若输出的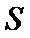
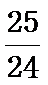
正确答案
解析
由题可知,S=S+1/n=1/2+1/4+1/6+1/8=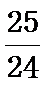
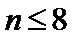
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
本题考查程序框图,解题步骤如下:代值依次判断即可.
易错点
本题易在判断条件时发生错误。
知识点
2. 设


正确答案
解析
将a,b取值一正一负,即可验证。
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
利用特值法即可求解
易错点
本题易在验证不等式时发生错误。
知识点
4. 有3个活动小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学在同一个兴趣小组的概率为( )
正确答案
解析
由题可知:甲有3种选择,乙有3种选择,两人在同一个兴趣小组的可能性有3种,所以概率为
考查方向
解题思路
本题考查古典概型,解题思路如下:直接计算即可
易错点
本题必须注意方法数要表示正确
知识点
6. 函数


正确答案
解析
由题可知:A=1,T=π,则w=2,φ=-π/12.所以

A选项不正确,C选项不正确,D选项不正确,所以选B选项。
考查方向
解题思路
利用三角函数的图像性质,即可得到结果。
A选项不正确,C选项不正确,D选项不正确,所以选B选项。
易错点
本题易在表示待定系数时发生错误。
知识点
8. 已知函数


正确答案
解析
由题可知:


B选项不正确,C选项不正确,D选项不正确,所以选A选项。
考查方向
解题思路
本题考查分段函数的求值,解题思路如下:画图代值计算即可
易错点
本题必须注意定义域的变化
知识点
7. 已知抛物线


正确答案
解析
由题可知:F(1,0),渐近线为y=bx/a,利用点到直线的距离公式解得:离心率e=
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
考查方向
解题思路
利用圆锥曲线的图像性质,即可得到结果。
A选项不正确,B选项不正确,D选项不正确,所以选C选项。
易错点
本题易在表示待定系数时发生错误。
知识点
9. 复数
正确答案
-i
解析

考查方向
解题思路
直接计算,即可得到结果。
易错点
本题易在求共轭复数时发生错误。
知识点
10. 若一个球的体积是
正确答案
128
解析
由题可知,球的半径为4,则正方体的棱长为a,3a2=64,所以表面积为128.
考查方向
解题思路
表示球内接正方体的棱长,即可得到结果。
易错点
本题易在求棱长时发生错误。
知识点
11. 在等比数列




正确答案
3
解析
由题可知,a5=3a1+2a3,q4=3+2q2,q2=3,则
考查方向
解题思路
表示等差数列,表示首项与公比的关系,代入即可得到结果。
易错点
本题易在表示等差数列时发生错误。
知识点
13. 已知圆

若




正确答案
解析
由题可知,圆心到l1的距离为d=√2,则圆心到l2的距离为√3,代入点到直线的距离公式,可求得k=
考查方向
解题思路
利用垂径定理求解即可
易错点
本题易在表示弦长时发生错误。
知识点
14.在直角梯形中










正确答案
5
解析
由题可知,以A为原点建系,

F(1/λ,√3),所以
考查方向
解题思路
1、画出平面图形并利用坐标系分析;2、表示平面向量,即可得到结果。
易错点
本题易在表示平面向量时发生错误。
知识点
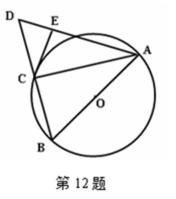
12. 如图,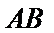
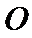
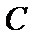
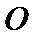
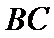
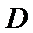
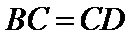
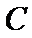
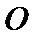
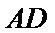
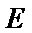
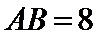
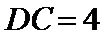
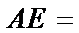
正确答案
3
解析
由题可知,a5=3a1+2a3,q4=3+2q2,q2=3,则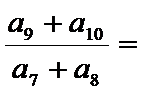
考查方向
解题思路
表示等差数列,表示首项与公比的关系,代入即可得到结果。
易错点
本题易在表示等差数列时发生错误。
知识点
15.在




(Ⅰ)求
(Ⅱ)若





正确答案
(1)

解析
试题分析:本题属于三角函数中的基本问题,题目的难度是逐渐由易到难.
(1)

又A为钝角
(2)由(1),得


由余弦定理
即

将①代入②,得

考查方向
解题思路
本题考查解三角形问题,解题步骤如下:1、利用两角和差公式化简求解。2、利用余弦定理求解。
易错点
注意角度的范围,忽视则容易出错。
知识点
17.如图所示,四边形







(Ⅰ)求证:
(Ⅱ)求

(III)求三棱锥
正确答案
见解析
解析
试题分析:本题属于立体几何中的基本问题,题目的难度是逐渐由易到难.
(1)证明:取AB中点O,连结OD,OE








又



(2)





在
又

(3)解:
考查方向
解题思路
本题考查立体几何中的线面位置关系,解题步骤如下:1、利用线面垂直的性质定理。2、利用向量法转化。
易错点
1、第一问中的线线垂直的判定。2、第二问中求线面角时要利用向量法。
知识点
16.福州市某家电超市为了使每天销售空调和冰箱获得的总利润达到最大,对某天即将出售的空调和冰箱进行了相关调查,得出下表:
问:该商场如果根据调查得来的数据,应该怎样确定每天空调和冰箱的供应量,才能使商场获得
的总利润最大?总利润的最大值为多少元?
正确答案
13
解析
由题可知,求出阴影区域的三个端点坐标,分别代入目标函数计算,即可求出最大值。
解:设每天调进空调和冰箱分别为


目标函数是
把直线

解方程
此时最大利润
答:空调和冰箱的供应量分别为2,3台,总利润为最大,最大为13百元.
考查方向
解题思路
1、表示平面区域;2、求出区域的端点坐标,即可得到结果。
易错点
本题易在表示平面区域时发生错误。
知识点
19.椭圆








(Ⅰ)求椭圆
(Ⅱ)设直线






正确答案
(1)

解析
试题分析:本题属于圆锥曲线中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求(2)要注意对参数的讨论.
(1)



(2)由(1)知

可设椭圆
设直线




因为直线


由韦达定理:

又


所以

当且仅当
此时
代入



考查方向
解题思路
本题考查圆锥曲线与直线的位置关系,解题步骤如下:1、利用e和c求a,b。2、联立直线与椭圆方程求解。
易错点
第二问中的分类讨论。
知识点
20.已知函数
(Ⅰ)若曲线



(Ⅱ)求证:函数

(III)若斜率为






正确答案
(1)3;(2)、(3)见解析.
解析
试题分析:本题属于导数应用中的基本问题,题目的难度是逐渐由易到难,(1)直接按照步骤来求;(2)要注意对参数的讨论.
(1) 





解得
(2) 



所以函数

(3)设点



要证
即证

即证

设
由(2)知


所以

即

考查方向
解题思路
本题考查导数的性质,解题步骤如下:1、求导,然后解导数不等式,求单调区间。2、对参数分类讨论求得零点个数。
易错点
第二问中的易丢对a的分类讨论。
知识点
18. 已知数列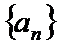
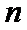
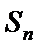
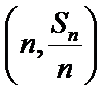
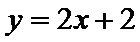
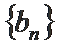
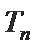
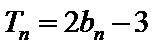
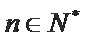
(Ⅰ)求数列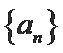
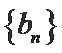
(Ⅱ)设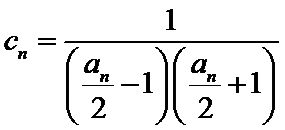
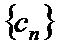
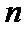
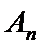
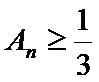
正确答案
(1)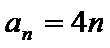
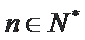
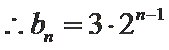
解析
试题分析:本题属于数列中的基本问题,题目的难度是逐渐由易到难.
解:(Ⅰ)由题意,得 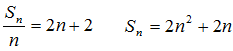
当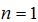
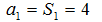
当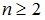
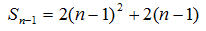
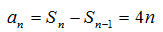
综上,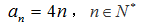
又
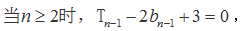
数列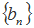
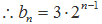
(Ⅱ)
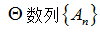
考查方向
解题思路
本题考查数列问题,解题步骤如下:
1、利用an与Sn的关系求解。
2、利用等比数列的求和公式求解。
易错点
等比数列分项时项数易错。