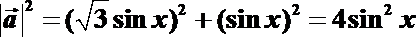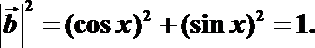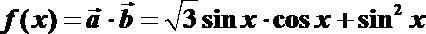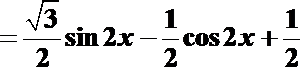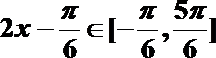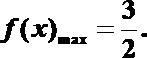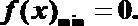- 真题试卷
- 模拟试卷
- 预测试卷
3. 若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5. 若函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
1. 设集合

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2. 若复数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4. 已知向量



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10. 设


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.“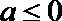
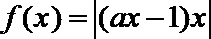
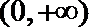
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
7. 设函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9. 函数

的图象重合,则
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11. 已知函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
12. 已知函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
16. 在平面直角坐标系






正确答案
-1或
解析
解析已在路上飞奔,马上就到!
知识点
13.已知向量

正确答案
5
解析
解析已在路上飞奔,马上就到!
知识点
14. 若函数



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
15. 若存在正数


正确答案
a>1
解析
解析已在路上飞奔,马上就到!
知识点
18.设向量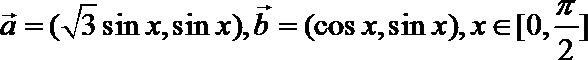
(Ⅰ)若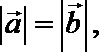
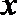
(Ⅱ)设函数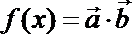
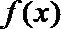
正确答案
(Ⅰ)由
由题意,得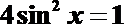
又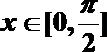

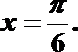
(Ⅱ)
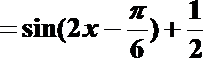
由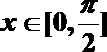
故 当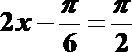
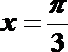
当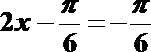
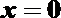
故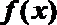
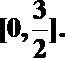
解析
解析已在路上飞奔,马上就到!
知识点
21.如图,游客从某旅游景区的景点






















(Ⅰ)求索道
(Ⅱ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅲ)为使两位游客在

正确答案
(Ⅱ)由(Ⅰ)知: 


所以由余弦定理得,
即

所以


故


∴为使两位游客在


解法二:(Ⅰ)如图作BD⊥CA于点D,
设BD=20k,则DC=25k,AD=48k,AB=52k
由AC=63k=1260m,知:AB=52k=1040m.
(Ⅱ)设乙出发x分钟后到达点M,
此时甲到达N点,如图所示.
则:AM=130x,AN=50(x+2),
由余弦定理得:MN2=AM2+AN2-2 AM·ANcosA=7400 x2-14000 x+10000,
其中0≤x≤8,当x=
此时乙在缆车上与甲的距离最短.
解析
解析已在路上飞奔,马上就到!
知识点
20.在



(Ⅰ)求
(Ⅱ)若


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 设函数
(Ⅰ)判断
(Ⅱ)当


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.已知函数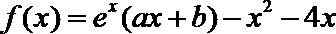
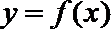
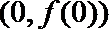
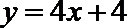
(Ⅰ)求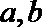
(Ⅱ)求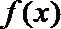
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知函数
其中
(Ⅰ)讨论

(Ⅱ)求证:在(Ⅰ)条件下
(Ⅲ)是否存在实数



正确答案
解析
解析已在路上飞奔,马上就到!